题目内容
高中流行这样一句话“文科就怕数学不好，理科就怕英语不好”．下
表是一次针对高三文科学生的调查所得的数据，试问：在出错概率不超过0.01的前提下文
科学生总成绩不好与数学成绩不好有关系吗？
| | 总成绩好 | 总成绩不好 | 总计 |
| 数学成绩好 | 20 | 10 | 30 |
| 数学成绩不好 | 5 | 15 | 20 |
| 总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05，P(K2≥6.635)≈0.01)
文科学生总成绩不好与数学成绩不好有关系.
解析试题分析：本小题独立性检测的应用，本小题的关键是计算出
的观测值
,选择合适的临界值
，然后根据计算出，并判断其与的大小关系，得出结论.
试题解析：依题意，计算K2的观测值：k＝
≈8.333＞6.635.
∵P(K2≥6.635)＝0.01，∴犯错误的概率不超过0.01.所以在犯错误的概率不超过0.01的前提下，认为“文科学生总成绩不好与数学成绩不好有关系”．
考点：独立性检测.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某汽车厂生产的A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆）
| | 轿车A | 轿车B | 轿车C |
| 舒适性 | 800 | 450 | 200 |
| 标准型 | 100 | 150 | 300 |
（Ⅰ）在这个月生产的轿车中，用分层抽样的方法抽取n辆，其中有A类轿车45辆，求n的值；
（Ⅱ）在C类轿车中，用分层抽样的方法抽取一个容量为5的样本，将该样本看成一个总体，从中任取2辆，求至少1辆舒适型轿车的概率；
（Ⅲ）用随机抽样的方法从A类舒适型轿车中抽取10辆，经检测它们的得分如下：，8.7，9.3，8.2，9.4，8.6，9.2，9.6，9.0，8.4，8.6，把这10辆轿车的得分看作一个总体，从中任取一个数，求该数与总体平均数之差的绝对值超过0.6的概率．
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数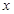 （个） | 2 | 3 | 4 | 5 |
加工的时间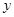 （小时） | 2.5 | 3 | 4 | 4.5 |
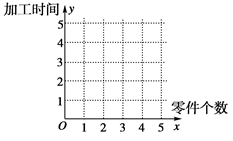
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出
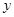关于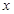的线性回归方程
，并在坐标系中画出回归直线；（3）试预测加工
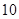个零件需要多少时间？参考公式：回归直线
，其中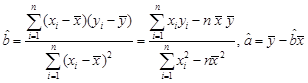
.
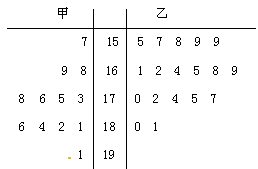
随机抽取某中学甲、乙两班各10名同学，测量他们的身高（单位：cm）获得身高数据如下：
| 甲班： | 158 | 168 | 162 | 168 | 163 | 170 | 182 | 179 | 171 | 179 |
| 乙班： | 159 | 168 | 162 | 170 | 165 | 173 | 176 | 181 | 178 | 179 |
（1）完成数据的茎叶图（以百位十位为茎，以个位为叶），并求甲班样本数据的中位数、众数；
（2）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率。
为调查某市老年人是否需要志愿者提供帮助，用简单随机抽样方法从该市调查了500位老年人，结果如右表.
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
（1）估计该市老年人中， 需要志愿者提供帮助的老年人的比例；
（2）能否有99%的把握认为该市的老年人是否需要志愿者提供帮助与性别有关？
附：
(
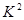
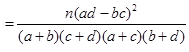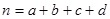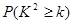） | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
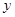（万元）和房屋的面积
（
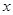）的数据 ，若由资料可知
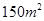时的销售价格.