题目内容
【题目】已知函数f(x)= ![]() 为偶函数.
为偶函数.
(1)求实数a的值;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=(lg 2)2+lg 2lg 5+lg 5﹣ ![]() ,判断λ与E的关系;
,判断λ与E的关系;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
](m>0,n>0)时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
【答案】
(1)解:函数f(x)= ![]() ,则f(﹣x)=
,则f(﹣x)= ![]() =
= ![]() ,
,
又由函数f(x)为偶函数,则有f(﹣x)=f(x),
即 ![]() =
= ![]() ,
,
解可得a=﹣1;
(2)解:由(1)可得a=﹣1,则f(x)= ![]() ,
,
则有f(1)=f(﹣1)=0,f(2)= ![]() ,
,
则集合E={y|y=f(x),x∈{﹣1,1,2}}={0, ![]() },
},
λ=(lg 2)2+lg 2lg 5+lg 5﹣ ![]() =lg2(lg2+lg5)+lg5﹣
=lg2(lg2+lg5)+lg5﹣ ![]() =lg2+lg5﹣
=lg2+lg5﹣ ![]() =
= ![]() ,
,
则有λ∈E;
(3)解:由(1)可得a=﹣1,则f(x)= ![]() =1﹣
=1﹣ ![]() ,则函数在(0,+∞)为增函数,
,则函数在(0,+∞)为增函数,
若当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,函数f(x)的值域为[2﹣3m,2﹣3n],
](m>0,n>0)时,函数f(x)的值域为[2﹣3m,2﹣3n],
则有 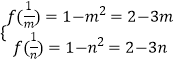 ,
,
解可得m= ![]() ,n=
,n= ![]() ,
,
又由 ![]() <
< ![]() 且m>0,n>0,则有0<n<m,
且m>0,n>0,则有0<n<m,
则m= ![]() ,n=
,n= ![]() .
.
【解析】(1)根据题意,由函数奇偶性的性质建立方程 ![]() =
= ![]() ,解可得a的值;(2)由(1)可得a的值,即可得函数的解析式,由此可得集合E,由对数的运算性质计算可得λ的值,分析可得答案;(3)由(1)可得函数的解析式,进而可以断函数的单调性,结合函数的值域建立方程关系进行求解即可.
,解可得a的值;(2)由(1)可得a的值,即可得函数的解析式,由此可得集合E,由对数的运算性质计算可得λ的值,分析可得答案;(3)由(1)可得函数的解析式,进而可以断函数的单调性,结合函数的值域建立方程关系进行求解即可.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

 小学能力测试卷系列答案
小学能力测试卷系列答案