题目内容
极坐标系与直角坐标系xOy有相同的长度单位,以原点D为极点,以x轴正半轴为极轴,曲线Cl的极坐标方程为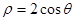 ,曲线C2的参数方程为
,曲线C2的参数方程为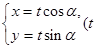 为参数)。
为参数)。
(1)当 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标;
(2)若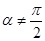 ,当
,当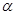 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
【答案】
(1)(0,0)或(1,1)
(2)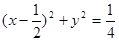 ,以
,以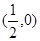 为圆心,
为圆心,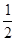 为半径的圆,除去点(0,0)
为半径的圆,除去点(0,0)
【解析】
试题分析:(1)根据题意,由于曲线Cl的极坐标方程为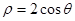 ,表示的为
,表示的为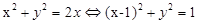
曲线C2的参数方程为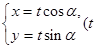 为参数))当
为参数))当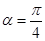 时,直线方程为y=x,联立方程组可知,交点坐标为(0,0)或(1,1)
时,直线方程为y=x,联立方程组可知,交点坐标为(0,0)或(1,1)
(2)由于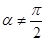 ,当
,当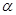 变化时,设曲线C1与C2的公共点为A,B ,那么可知利用直角三角形的性质可知AB中点M轨迹方程为
变化时,设曲线C1与C2的公共点为A,B ,那么可知利用直角三角形的性质可知AB中点M轨迹方程为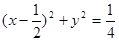 ,以
,以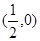 为圆心,
为圆心,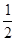 为半径的圆,除去点(0,0)
为半径的圆,除去点(0,0)
考点:参数方程
点评:主要是考查了参数方程以及直角坐标方程的运用,属于基础题。

练习册系列答案
相关题目
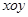 有相同的长度单位,以原点
有相同的长度单位,以原点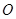 为极点,以
为极点,以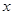 轴正半轴为极轴.已知直线
轴正半轴为极轴.已知直线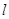 的参数方程为
的参数方程为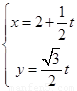 (
(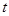 为参数),曲线
为参数),曲线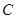 的极坐标方程为
的极坐标方程为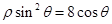 .
.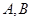 两点,求弦长
两点,求弦长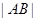 .
.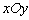 有相同的长度单位,以原点
有相同的长度单位,以原点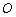 为极点,以
为极点,以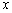 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线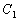 的极坐标方程为
的极坐标方程为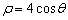 ,曲线
,曲线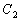 的参数方程是
的参数方程是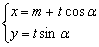 (
(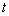 为参数,
为参数,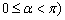 ,射线
,射线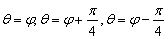 与曲线
与曲线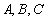
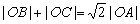 ;
;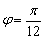 时,
时,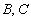 两点在曲线
两点在曲线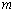 与
与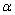 的值.
的值.