题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| c2 |
| 4 |
(1)若椭圆C经过两点(1,
4
| ||
| 3 |
3
| ||
| 2 |
(2)当c为定值时,求证:直线MN经过一定点E,并求
| OP |
| OE |
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围.
分析:(1)令椭圆mx2+ny2=1,得
,由此能求出椭圆方程.
(2)直线AB:
+
=1,设点P(x0,y0),点O,M,P,N所在的圆的方程为x2-x0x+y2-y0y=0,与圆x2+y2=
作差,即有直线MN:x0x+y0y=
,因为点P(x0,y0)在直线AB上,所以
+
=1,由此能求出
•
的值.
(3)由直线AB与圆G:x2+y2=
相离,知e4-6e2+4>0.因为0<e<1,所以0<e2<3-
,连接ON,OM,OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以e4-3e2+1≤0.由此能求出椭圆离心率的取值范围.
|
(2)直线AB:
| x |
| -a |
| y |
| b |
| c2 |
| 4 |
| c2 |
| 4 |
| x0 |
| -a |
| y0 |
| b |
| OP |
| OE |
(3)由直线AB与圆G:x2+y2=
| c2 |
| 4 |
| 5 |
解答: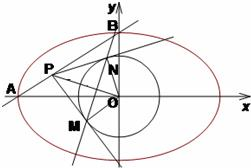 解:(1)令椭圆mx2+ny2=1,其中m=
解:(1)令椭圆mx2+ny2=1,其中m=
,n=
,
得
,所以m=
,n=
,即椭圆为
+
=1. …(3分)
(2)直线AB:
+
=1,
设点P(x0,y0),则OP中点为(
,
),
所以点O,M,P,N所在的圆的方程为(x-
)2+(y-
)2=
,
化简为x2-x0x+y2-y0y=0,…(5分)
与圆x2+y2=
作差,即有直线MN:x0x+y0y=
,
因为点P(x0,y0)在直线AB上,所以
+
=1,
所以x0(x+
y)+(by-
)=0,所以
,
得x=-
,y=
,故定点E(-
,
),…(8分)
•
=(x0,
x0+b)•(-
,
)=
. …(9分)
(3)由直线AB与圆G:x2+y2=
(c是椭圆的焦半距)相离,
则
>
,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),
得e4-6e2+4>0
因为0<e<1,所以0<e2<3-
,①…(11分)
连接ON,OM,OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,
所以
≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0
因为0<e<1,所以
≤e2<1,②…(14分)
由①②,
≤e2<3-
,
所以
≤e<
. …(15分)
 解:(1)令椭圆mx2+ny2=1,其中m=
解:(1)令椭圆mx2+ny2=1,其中m=| 1 |
| a2 |
| 1 |
| b2 |
得
|
| 1 |
| 9 |
| 1 |
| 4 |
| x2 |
| 9 |
| y2 |
| 4 |
(2)直线AB:
| x |
| -a |
| y |
| b |
设点P(x0,y0),则OP中点为(
| x0 |
| 2 |
| y0 |
| 2 |
所以点O,M,P,N所在的圆的方程为(x-
| x0 |
| 2 |
| y0 |
| 2 |
| ||
| 4 |
化简为x2-x0x+y2-y0y=0,…(5分)
与圆x2+y2=
| c2 |
| 4 |
| c2 |
| 4 |
因为点P(x0,y0)在直线AB上,所以
| x0 |
| -a |
| y0 |
| b |
所以x0(x+
| b |
| a |
| c2 |
| 4 |
|
得x=-
| c2 |
| 4a |
| c2 |
| 4b |
| c2 |
| 4a |
| c2 |
| 4b |
| OP |
| OE |
| b |
| a |
| c2 |
| 4a |
| c2 |
| 4b |
| c2 |
| 4 |
(3)由直线AB与圆G:x2+y2=
| c2 |
| 4 |
则
| ab | ||
|
| c |
| 2 |
得e4-6e2+4>0
因为0<e<1,所以0<e2<3-
| 5 |
连接ON,OM,OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,
所以
| ab | ||
|
因为0<e<1,所以
3-
| ||
| 2 |
由①②,
3-
| ||
| 2 |
| 5 |
所以
| ||
| 2 |
| ||||
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目