题目内容
在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:利用等体积法,VA-MBD=VB-AMD.求出MDB的面积,然后求距离即可.
解答: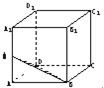 解:A到面MBD的距离由等积变形可得.
解:A到面MBD的距离由等积变形可得.
VA-MBD=VB-AMD.即:
a3=
×d×
×
a×
即易求d=
a.
故选D
 解:A到面MBD的距离由等积变形可得.
解:A到面MBD的距离由等积变形可得.VA-MBD=VB-AMD.即:
| 1 |
| 12 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
|
| ||
| 6 |
故选D
点评:本题考查点到平面的距离,等体积法求距离的方法,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

