题目内容
【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
【答案】见解析
【解析】解 (1)函数的定义域为[0,+∞),
f′(x)=![]() +
+![]() =
=![]() (x>0).
(x>0).
若a≤0,则f′(x)>0,f(x)有单调递增区间[0,+∞).
若a>0,令f′(x)=0,得x=![]() ,
,
当0<x<![]() 时,f′(x)<0,
时,f′(x)<0,
当x>![]() 时,f′(x)>0.
时,f′(x)>0.
f(x)有单调递减区间[0,![]() ],有单调递增区间(
],有单调递增区间(![]() ,+∞).
,+∞).
(2)①由(1)知,若a≤0,f(x)在[0,2]上单调递增,
所以g(a)=f(0)=0.
若0<a<6,f(x)在[0,![]() ]上单调递减,在(
]上单调递减,在(![]() ,2]上单调递增,
,2]上单调递增,
所以g(a)=f(![]() )=-
)=-![]()
![]() .
.
若a≥6,f(x)在[0,2]上单调递减,所以g(a)=f(2)=![]() (2-a).
(2-a).
综上所述,g(a)=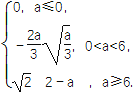
②令-6≤g(a)≤-2.若a≤0,无解.
若0<a<6,解得3≤a<6.
若a≥6,解得6≤a≤2+3![]() .
.
故a的取值范围为3≤a≤2+3![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目