题目内容
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍。设购进A掀电脑x台,这100台电脑的销售总利润为y元。
①求y与x的关系式;
②该商店购进A型、B型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台。若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案。
【答案】(1)每台A型电脑的销售利润为100元,每台B型电脑的销售利润为150元;(2)商店购进A型电脑34台,B型电脑66台,才能使销售总利润最大;(3)即商店购进70台A型电脑和30台B型电脑才能获得最大利润.
【解析】试题分析:(1)依据题设条件每台A型电脑的销售利润为a元,每台B型电脑的销售利润为b元建立方程组![]() 进行求解;(2)①根据题意建立目标函数y=100x+150(100-x);②根据题意建立不等式100-x≤2x进行分析求解;(3)据题意建立目标函数y=(100+m)x+150(100-x),然后运用分类整合思想对参数进行分类讨论求其最大值。
进行求解;(2)①根据题意建立目标函数y=100x+150(100-x);②根据题意建立不等式100-x≤2x进行分析求解;(3)据题意建立目标函数y=(100+m)x+150(100-x),然后运用分类整合思想对参数进行分类讨论求其最大值。
解:(1)设每台A型电脑的销售利润为a元,每台B型电脑的销售利润为b元,
则有![]() 解得
解得![]()
即每台A型电脑的销售利润为100元,每台B型电脑的销售利润为150元.
(2)①根据题意得y=100x+150(100-x),即y=-50x+15000
②根据题意得100-x≤2x,解得x≥33![]() ,
,
∵y=-50x+15000,-50<0,∴y随x的增大而减小.
∵x为正整数,∴当x=34最小时,y取最大值,此时100-x=66.
即商店购进A型电脑34台,B型电脑66台,才能使销售总利润最大
(3)根据题意得y=(100+m)x+150(100-x),即y=(m-50)x+15000.
33![]() ≤x≤70.
≤x≤70.
①当0<m<50时,m-50<0,y随x的增大而减小.
∴当x =34时,y取得最大值.
即商店购进34台A型电脑和66台B型电脑才能获得最大利润;
②当m=50时,m-50=0,y=15000.
即商店购进A型电脑数最满足33![]() ≤x≤70的整数时,均获得最大利润;
≤x≤70的整数时,均获得最大利润;
③当50<m<100时,m-50>0,y随x的增大而增大.
∴x=70时,y取得最大值.
即商店购进70台A型电脑和30台B型电脑才能获得最大利润.

【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 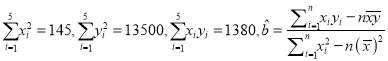 .
.