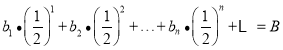题目内容
【题目】已知函数![]() ,若
,若![]() 在区间[2,3]上有最大值1.
在区间[2,3]上有最大值1.
(1)求![]() 的值;
的值;
(2)求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3)若![]() 在[2,4]上单调,求实数
在[2,4]上单调,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3)![]()
【解析】
(1)根据二次函数对称轴以及在区间![]() 上的最大值列方程,求得
上的最大值列方程,求得![]() 的值.(2)利用二次函数对称轴和开口方向,求得函数的最大值和最小值,由此求得函数值域.(3)利用二次函数对称轴与
的值.(2)利用二次函数对称轴和开口方向,求得函数的最大值和最小值,由此求得函数值域.(3)利用二次函数对称轴与![]() 的位置关系,根据
的位置关系,根据![]() 的单调性,求得
的单调性,求得![]() 的取值范围.
的取值范围.
(1)由于二次函数开口向下,且对称轴为![]() ,所以函数
,所以函数![]() 在
在![]() 上递减,故
上递减,故![]() ,解得
,解得![]() .所以
.所以![]() .
.
(2)由(1)知![]() ,且函数开口向下,对称轴
,且函数开口向下,对称轴![]() ,故函数
,故函数![]() 在
在![]() 时取得最小值为
时取得最小值为![]() ,在
,在![]() 时取得最大值为
时取得最大值为![]() ,所以函数的值域为
,所以函数的值域为![]() .
.
(3)依题意![]() 在
在![]() 上单调,由于函数
上单调,由于函数![]() 的对称轴为
的对称轴为![]() ,所以
,所以![]() 或
或![]() ,解得
,解得![]() .故
.故![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】![]() 市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-
市积极倡导学生参与绿色环保活动,其中代号为“环保卫士-![]() ”的绿色环保活动小组对
”的绿色环保活动小组对![]() 年
年![]() 月-
月-![]() 年
年![]() 月(一月)内空气质量指数
月(一月)内空气质量指数![]() 进行监测,如表是在这一年随机抽取的
进行监测,如表是在这一年随机抽取的![]() 天的统计结果:
天的统计结果:
指数 |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻微污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(Ⅰ)若![]() 市某企业每天由空气污染造成的经济损失
市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: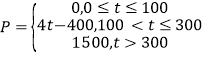 ,,在这一年内随机抽取一天,估计该天经济损失
,,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(Ⅱ)若本次抽取的样本数据有![]() 天是在供暖季节,其中有
天是在供暖季节,其中有![]() 天为重度污染,完成
天为重度污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为
的把握认为![]() 市本年度空气重度污染与供暖有关?
市本年度空气重度污染与供暖有关?

下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.