题目内容
 如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=
如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=| 3 |
(1)写出△AOB的面积关于α的函数关系式f(α);
(2)写出函数f(α)的取值范围.
分析:(1)根据OE=1,EF=
,可得∠EOF=60°.由于A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,∠AOE=α,故要进行分类讨论:当α∈[0,
]时,△AOB的两顶点A、B在E、F上;当a∈(
,
]时,A点在EF上,B点在FG上,从而可求相应的面积f(α),进而得出结论;
(2)由(1)分类求函数的值域:当α∈[0,
]时,f(α)=
∈[
,
-1];当α∈(
,
]时,f(α)=
∈[
-
,
].故可得结论.
| 3 |
| π |
| 12 |
| π |
| 12 |
| π |
| 4 |
(2)由(1)分类求函数的值域:当α∈[0,
| π |
| 12 |
| ||||
2cos(2α+
|
| 1 |
| 2 |
| 3 |
| π |
| 12 |
| π |
| 4 |
| ||||
2cos(2α-
|
| 6 |
| 3 |
| ||
| 2 |
解答: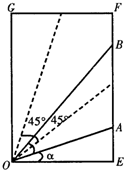 解:(1)∵OE=1,EF=
解:(1)∵OE=1,EF=
.
∴∠EOF=60°.
当α∈[0,
]时,△AOB的两顶点A、B在E、F上,
且AE=tanα,BE=tan(45°+α).
∴f(α)=S△AOB=
[tan(45°+α)-tanα]
=
=
.
当a∈(
,
]时,A点在EF上,B点在FG上,且OA=
,OB=
.
∴f(α)=S△AOB=
OA•OB•sin45°=
•
•sin45°=
综上得:f(α)=
(2)由(1)得:当α∈[0,
]时,f(α)=
∈[
,
-1].
且当α=0时,f(α)min=
;α=
时,f(α)max=
-1;
当α∈(
,
]时,-
≤2α-
≤
,f(α)=
∈[
-
,
].
且当α=
时,f(α) min=
-
;当α=
时,f(α) max=
.
所以f(α)∈[
,
].
 解:(1)∵OE=1,EF=
解:(1)∵OE=1,EF=| 3 |
∴∠EOF=60°.
当α∈[0,
| π |
| 12 |
且AE=tanα,BE=tan(45°+α).
∴f(α)=S△AOB=
| 1 |
| 2 |
=
| sin45° |
| 2cosα•cos(45°+α) |
| ||
2cos(2α+45°)+
|
当a∈(
| π |
| 12 |
| π |
| 4 |
| 1 |
| cosα |
| ||
| cos(45°-α) |
∴f(α)=S△AOB=
| 1 |
| 2 |
| 1 |
| 2cosα |
| ||
| cos(45°-α) |
| ||||
2cos(
|
综上得:f(α)=
|
(2)由(1)得:当α∈[0,
| π |
| 12 |
| ||||
2cos(2α+
|
| 1 |
| 2 |
| 3 |
且当α=0时,f(α)min=
| 1 |
| 2 |
| π |
| 12 |
| 3 |
当α∈(
| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| π |
| 4 |
| π |
| 4 |
| ||||
2cos(2α-
|
| 6 |
| 3 |
| ||
| 2 |
且当α=
| π |
| 8 |
| 6 |
| 3 |
| π |
| 4 |
| ||
| 2 |
所以f(α)∈[
| 1 |
| 2 |
| ||
| 2 |
点评:本题以实际问题为载体,考查函数模型的构建,考查三角函数,同时考查了三角函数的值域问题,综合性强,其中分类讨论是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
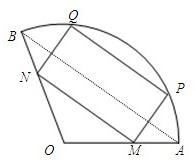 如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
 ,设∠AOE=α.
,设∠AOE=α.
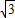 ,设∠AOE=α.
,设∠AOE=α.