题目内容
如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=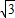 ,设∠AOE=α.
,设∠AOE=α.(1)写出△AOB的面积关于α的函数关系式f(α);
(2)写出函数f(α)的取值范围.

【答案】分析:(1)根据OE=1,EF= ,可得∠EOF=60°.由于A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,∠AOE=α,故要进行分类讨论:当α∈[0,
,可得∠EOF=60°.由于A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,∠AOE=α,故要进行分类讨论:当α∈[0,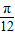 ]时,△AOB的两顶点A、B在E、F上;当a∈
]时,△AOB的两顶点A、B在E、F上;当a∈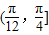 时,A点在EF上,B点在FG上,从而可求相应的面积f(α),进而得出结论;
时,A点在EF上,B点在FG上,从而可求相应的面积f(α),进而得出结论;
(2)由(1)分类求函数的值域:当α∈[0,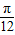 ]时,f(α)=
]时,f(α)=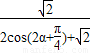 ∈[
∈[ ,
,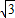 -1];当α∈
-1];当α∈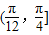 时,f(α)=
时,f(α)=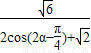 ∈[
∈[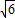 -
-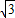 ,
,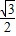 ].故可得结论.
].故可得结论.
解答: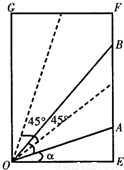 解:(1)∵OE=1,EF=
解:(1)∵OE=1,EF=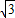 .
.
∴∠EOF=60°.
当α∈[0,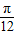 ]时,△AOB的两顶点A、B在E、F上,
]时,△AOB的两顶点A、B在E、F上,
且AE=tanα,BE=tan(45°+α).
∴f(α)=S△AOB= [tan(45°+α)-tanα]
[tan(45°+α)-tanα]
=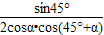 =
=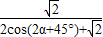 .
.
当a∈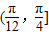 时,A点在EF上,B点在FG上,且OA=
时,A点在EF上,B点在FG上,且OA=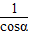 ,OB=
,OB=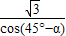 .
.
∴f(α)=S△AOB= OA•OB•sin45°=
OA•OB•sin45°=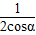 •
•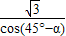 •sin45°=
•sin45°=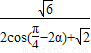
综上得:f(α)=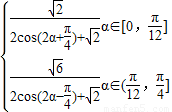
(2)由(1)得:当α∈[0,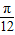 ]时,f(α)=
]时,f(α)=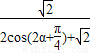 ∈[
∈[ ,
,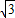 -1].
-1].
且当α=0时,f(α)min= ;α=
;α=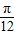 时,f(α)max=
时,f(α)max=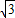 -1;
-1;
当α∈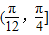 时,-
时,-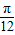 ≤2α-
≤2α-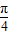 ≤
≤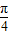 ,f(α)=
,f(α)=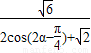 ∈[
∈[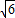 -
-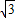 ,
,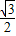 ].
].
且当α=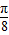 时,f(α) min=
时,f(α) min=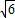 -
-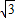 ;当α=
;当α=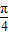 时,f(α) max=
时,f(α) max=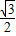 .
.
所以f(α)∈[ ,
,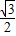 ].
].
点评:本题以实际问题为载体,考查函数模型的构建,考查三角函数,同时考查了三角函数的值域问题,综合性强,其中分类讨论是解题的关键.
 ,可得∠EOF=60°.由于A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,∠AOE=α,故要进行分类讨论:当α∈[0,
,可得∠EOF=60°.由于A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,∠AOE=α,故要进行分类讨论:当α∈[0,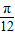 ]时,△AOB的两顶点A、B在E、F上;当a∈
]时,△AOB的两顶点A、B在E、F上;当a∈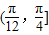 时,A点在EF上,B点在FG上,从而可求相应的面积f(α),进而得出结论;
时,A点在EF上,B点在FG上,从而可求相应的面积f(α),进而得出结论;(2)由(1)分类求函数的值域:当α∈[0,
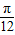 ]时,f(α)=
]时,f(α)=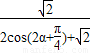 ∈[
∈[ ,
,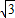 -1];当α∈
-1];当α∈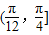 时,f(α)=
时,f(α)=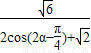 ∈[
∈[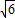 -
-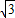 ,
,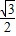 ].故可得结论.
].故可得结论.解答:
 解:(1)∵OE=1,EF=
解:(1)∵OE=1,EF=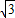 .
.∴∠EOF=60°.
当α∈[0,
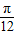 ]时,△AOB的两顶点A、B在E、F上,
]时,△AOB的两顶点A、B在E、F上,且AE=tanα,BE=tan(45°+α).
∴f(α)=S△AOB=
 [tan(45°+α)-tanα]
[tan(45°+α)-tanα]=
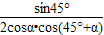 =
=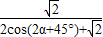 .
.当a∈
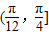 时,A点在EF上,B点在FG上,且OA=
时,A点在EF上,B点在FG上,且OA=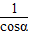 ,OB=
,OB=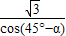 .
.∴f(α)=S△AOB=
 OA•OB•sin45°=
OA•OB•sin45°=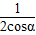 •
•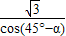 •sin45°=
•sin45°=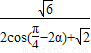
综上得:f(α)=
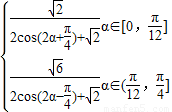
(2)由(1)得:当α∈[0,
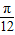 ]时,f(α)=
]时,f(α)=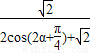 ∈[
∈[ ,
,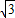 -1].
-1].且当α=0时,f(α)min=
 ;α=
;α=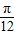 时,f(α)max=
时,f(α)max=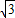 -1;
-1;当α∈
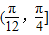 时,-
时,-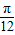 ≤2α-
≤2α-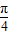 ≤
≤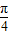 ,f(α)=
,f(α)=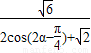 ∈[
∈[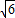 -
-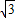 ,
,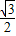 ].
].且当α=
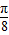 时,f(α) min=
时,f(α) min=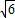 -
-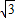 ;当α=
;当α=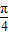 时,f(α) max=
时,f(α) max=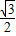 .
.所以f(α)∈[
 ,
,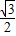 ].
].点评:本题以实际问题为载体,考查函数模型的构建,考查三角函数,同时考查了三角函数的值域问题,综合性强,其中分类讨论是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
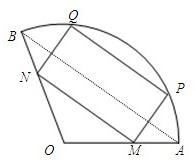 如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少? 如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=
如图,A、B是一矩形OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=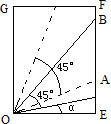
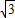 ,设∠AOE=α.
,设∠AOE=α.