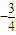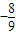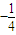题目内容
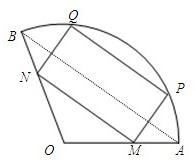 如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
如图,半径是1且圆心角为120°的扇形中,点A、B是扇形的两个端点,线段PQ是一条平行于弦AB的动弦,以PQ为一边作该扇形的一个内接矩形MNQP,将矩形MNQP面积记为S.试确定当P点在什么位置时,S取得最大,最大值是多少?
分析:要用三角函数解决问题,首先构造三角形即连接op,然后设出角∠AOP=θ,并过O作OH⊥MN于H,能推出H是MN的中点.然后在△OPM中,利用正弦定理得到MP,而MN=2HM,进而得到MN,利用三角形面积法求出S.利用三角函数变换公式得到正弦函数,最后求出正弦函数最大值即可.
解答: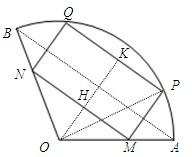 解:连接OP,设∠AOP=θ,则θ∈(0°,120°),
解:连接OP,设∠AOP=θ,则θ∈(0°,120°),
过点O作OH⊥MN于H,则H是MN的中点,(2分)
在△OMP中,由正弦定理有
=
=
所以MP=
sinθ①(5分)
OM=
sin(60°-θ),
所以在直角△OMH中,HM=OMsin60°=sin(60°-θ)
所以MN=2HM=2sin(60°-θ)②(8分)
所以由①②得:S=
sinθsin(60°-θ)=2sinθcosθ-
sin2θ(10分)
=sin2θ-
(1-cos2θ)=sin2θ+
cos2θ-
=
sin(2θ+30°)-
(13分)
因为θ∈(0°,120°),所以当2θ+30°=90°,
即θ=30°时Smax=
,(15分)
即
的长是
的长的
时(或说成当∠AOP=30°时),
S取得最大值
.(16分)
 解:连接OP,设∠AOP=θ,则θ∈(0°,120°),
解:连接OP,设∠AOP=θ,则θ∈(0°,120°),过点O作OH⊥MN于H,则H是MN的中点,(2分)
在△OMP中,由正弦定理有
| MP |
| sinθ |
| MO |
| sin(60°-θ) |
| 1 |
| sin120° |
所以MP=
| 2 | ||
|
OM=
| 2 | ||
|
所以在直角△OMH中,HM=OMsin60°=sin(60°-θ)
所以MN=2HM=2sin(60°-θ)②(8分)
所以由①②得:S=
| 4 | ||
|
| 2 | ||
|
=sin2θ-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
=
2
| ||
| 3 |
| ||
| 3 |
因为θ∈(0°,120°),所以当2θ+30°=90°,
即θ=30°时Smax=
| ||
| 3 |
即
 |
| AP |
 |
| AB |
| 1 |
| 4 |
S取得最大值
| ||
| 3 |
点评:此题考查正弦函数最值问题,学生的构造能力及三角函数的变换能力,解决实际问题的能力.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
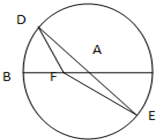 如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且
如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且| BF |
| FA |
| FD |
| FE |
A、-
| ||
B、-
| ||
C、-
| ||
| D、不确定 |
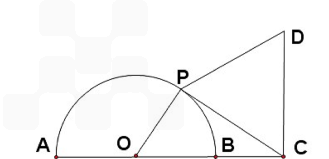
 ,点P是半圆上的动点,以
,点P是半圆上的动点,以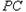 为边作等边三角形
为边作等边三角形 ,且点D与圆心分别在
,且点D与圆心分别在 的两侧.
的两侧. ,试将四边形
,试将四边形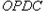 的面积
的面积 表示成
表示成 的函数;
的函数;  的面积的最大值.
的面积的最大值.
 的半径是1,点在直径AB的延长线上, BC=1, 点P是
的半径是1,点在直径AB的延长线上, BC=1, 点P是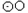 上半圆上的动点, 以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.
上半圆上的动点, 以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧.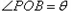 ,试将四边形OPDC的面积y表示成θ的函数;
,试将四边形OPDC的面积y表示成θ的函数; 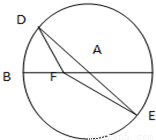 如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且
如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且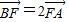 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则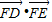 的值是( )
的值是( )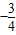
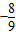
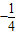
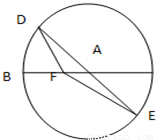 如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且
如图,BC是单位圆(即半径为1的圆)圆A的一条直径,F是线段AB上的一点,且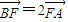 ,若DE是圆A中绕圆心A运动的一条直径,则
,若DE是圆A中绕圆心A运动的一条直径,则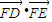 的值是( )
的值是( )