题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
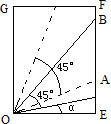
解:因为OE=1,EF= 当α∈[ 所以f(α)=S△AOB= 当α∈[ 所以f(α)=S△AOB= 综上,得f(α)= |
(2) |
解:由(1)得,当α∈[0, f(α)= 当α∈[ 故f(α)的取值范围为[ 分析:本题主要考查三角形的有关知识及三角函数在求函数最值方面的应用.由OE、EF的长知要讨论α的范围.再根据三角形的边角关系列出△AOB的面积,再求函数最值. |

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
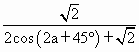
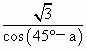 .
.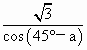 ·sin
·sin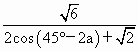
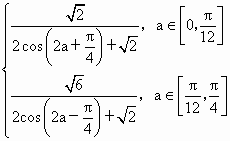
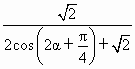 ∈
∈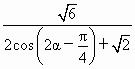 ∈
∈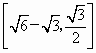 ,且当α=
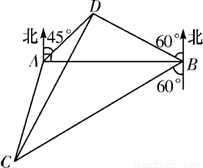
,且当α= 如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以
如图所示,A、B是在同一水平面上相距am的两处雷达站,A在B的正西方,突然两台雷达同时发现天空O位置处一不明飞行物正以