题目内容
(12分) 已知函数 =loga
=loga (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数
(1)求 ,(
,(
(2)讨论 在(1,+∞)上的单调性,并予以证明
在(1,+∞)上的单调性,并予以证明
【答案】
(1)
(2)当a>1时,f(x)=loga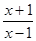 在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga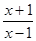 在(1,+∞)上为增函数
在(1,+∞)上为增函数
【解析】解:
(1)
(2)设u=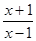 ,任取x2>x1>1,则
,任取x2>x1>1,则
u2-u1=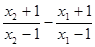
=
=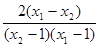 .
.
∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴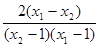 <0,即u2<u1.
<0,即u2<u1.
当a>1时,y=logax是增函数,∴logau2<logau1,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logau2>logau1,
即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga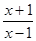 在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga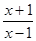 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.

练习册系列答案
相关题目
 的定义域为集合A,
的定义域为集合A,  的值域为集合B.
的值域为集合B. ,求
,求 ;
; ,求实数
,求实数 的取值范围。
的取值范围。 的导函数
的导函数 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上.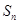 的最大值;
的最大值; ,其中
,其中 ,求
,求 的前
的前 是偶函数.
是偶函数. 有解,求m的取值范围.
有解,求m的取值范围.