题目内容
【题目】点P在双曲线 ![]() (a>0,b>0)的右支上,其左、右焦点分别为F1、F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为( )
(a>0,b>0)的右支上,其左、右焦点分别为F1、F2 , 直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2 , 则该双曲线的渐近线的斜率为( )
A.± ![]()
B.± ![]()
C.± ![]()
D.± ![]()
【答案】A
【解析】解:由线段PF1的垂直平分线恰好过点F2 , 可得|PF2|=|F1F2|=2c,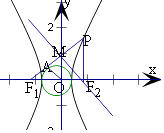
由直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,
可得|OA|=a,
设PF1的中点为M,由中位线定理可得|MF2|=2a,
在直角三角形PMF2中,可得|PM|= ![]() =2b,
=2b,
即有|PF1|=4b,
由双曲线的定义可得|PF1|﹣|PF2|=2a,
即4b﹣2c=2a,即2b=a+c,
即有4b2=(a+c)2 ,
即4(c2﹣a2)=(a+c)2 ,
可得a= ![]() c,b=
c,b= ![]() c,
c,
即有双曲线的渐近线方程y=± ![]() x,
x,
该双曲线的渐近线的斜率为± ![]() .
.
故选:A.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目


