��Ŀ����
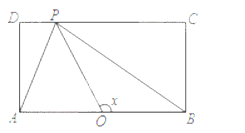
����Ŀ������ԲC�� ![]() ��a��b��0�������ҽ���ֱ�ΪF1��F2 �� �϶���ΪA����A��AF2��ֱ��ֱ�߽�x�Ḻ������Q�㣬��F1ǡ�����߶�QF2���е㣮
��a��b��0�������ҽ���ֱ�ΪF1��F2 �� �϶���ΪA����A��AF2��ֱ��ֱ�߽�x�Ḻ������Q�㣬��F1ǡ�����߶�QF2���е㣮
��1������A��Q��F2�����Բǡ����ֱ��3x��4y��7=0���У�����ԲC�ķ��̣�
��2���ڣ�1���������£�B����ԲC���㣬����R�� ![]() ��0������x��غϵ�ֱ��l����ԲC��E��F���㣬ֱ��BE��BF�ֱ�ֱ��x=
��0������x��غϵ�ֱ��l����ԲC��E��F���㣬ֱ��BE��BF�ֱ�ֱ��x= ![]() ��M��N���㣬��ֱ��MR��NR��б�ʷֱ�Ϊk1 �� k2 �� ���ʣ�k1k2�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵�����ɣ�
��M��N���㣬��ֱ��MR��NR��б�ʷֱ�Ϊk1 �� k2 �� ���ʣ�k1k2�Ƿ�Ϊ��ֵ�����ǣ�����ö�ֵ�������ǣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������֪A��0��b����F1���߶�QF1���е㣬
��F1����c��0����F2��c��0������Q����3c��0����
�ߡ�QAF1=90�㣬
��b2=3c2��
������Rt��QAF1���ԲԲ��Ϊб�ߵ�QF1�е�F1����c��0�����뾶����2c��
��A��Q��F2������ǡ����ֱ��3x��4y��7=0���У�
��F1����c��0����ֱ�ߵľ�����ڰ뾶2c��
�� ![]() =2c��
=2c��
��ã�c=1��b2=3��a2=4��
����Բ�ı����̣� ![]()
��2��
�⣺��E��x1��y1����F��x2��y2����
ֱ��PQ�ķ���Ϊx=my+ ![]() ��������Բ����
��������Բ���� 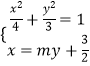 ��
��
4��4+3m2��y2+36my��21=0��
y1+y2=�� ![]() ��y1y2=��
��y1y2=�� ![]() ��
��
��B��E��M�����㹲�ߣ���֪�� ![]() =
= ![]() ����yM=
����yM= ![]() ��
��
ͬ���ɵã�yN= ![]() ��
��
��k1k2= ![]() ��
�� ![]() =
= ![]() =
= ![]() ��
��
��4��x1+2����x2+2��=��2my1+7����2my2+7��=4m2y1y2+14m��y1+y2��+49��
��k1k2=  =��
=�� ![]() ��
��
��k1k2�Ƿ�Ϊ��ֵ�� ![]()
����������1���������֪b2=3c2 �� ���ݵ㵽ֱ�ߵľ��빫ʽ���������c��ֵ�����a��b��ֵ�������Բ���̣���2����ֱ��PQ���̣�������Բ���̣�����Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ�����M��N��������꣬����б�ʹ�ʽ���k1 �� k2 �� ����Τ�ﶨ���������k1k2 ��
�����㾫����������Ŀ����֪������������Բ�ı����̵����֪ʶ���Եõ�����Ĵ𰸣���Ҫ������Բ�����̽�����x�![]() ��������y�
��������y�![]() ��
��