题目内容
已知ABCD是半径为2的圆的内接正方形,现在圆的内部随机取一点P,则点P落在正方形ABCD内部的概率为 .

试题分析:记事件“在圆的内部随机取一点P,点P落在正方形内的部分”为事件A,则事件A发生的概率为:P(A)=构成事件A的区域面积(即正方形的面积)与实验的全部结果所构成的区域面积(即圆的面积)的比值即可.解:设正方形的边长为a,圆的半径r=2,,由题意可得,42=2a2,即a=2
 ∴正方形的边长为2
∴正方形的边长为2 ,面积为S=8,∵内接圆的面积为S=4π,记事件“在圆的内部随机取一点P,点P落在正方形内的部分”为事件A,由几何概率公式可得:P(A)=
,面积为S=8,∵内接圆的面积为S=4π,记事件“在圆的内部随机取一点P,点P落在正方形内的部分”为事件A,由几何概率公式可得:P(A)=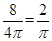 ,故可知答案
,故可知答案
点评:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.其求解通常转化为求解区域的长度、面积、体积等

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
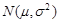 的随机变量,在区间
的随机变量,在区间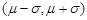 ,
,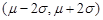 和
和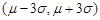 内取值的概率分别为
内取值的概率分别为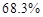 ,
,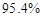 和
和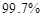 .某大型国有企业为
.某大型国有企业为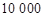 名员工定制工作服,设员工的身高(单位:
名员工定制工作服,设员工的身高(单位: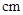 )服从正态分布
)服从正态分布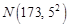 ,则适合身高在
,则适合身高在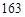 ~
~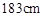 范围内员工穿的服装大约要定制( )
范围内员工穿的服装大约要定制( )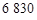 套
套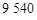 套
套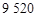 套
套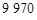 套
套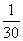


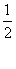
 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为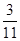 。
。 。
。
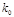
 在区间
在区间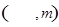 内取值的概率小于0.5;
内取值的概率小于0.5;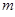 一定时,
一定时,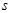 越小,曲线越“矮胖”;
越小,曲线越“矮胖”;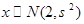 ,且
,且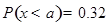 ,则
,则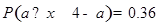

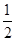
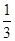

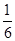
 ,则函数
,则函数 在
在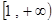 上为增函数的概率是 ( )
上为增函数的概率是 ( )
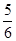

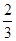
 ,
,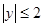 ,点
,点 的坐标为
的坐标为
 时,求
时,求 的概率。
的概率。 时,求
时,求