题目内容
(本小题满分14分)已知 ,
,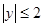 ,点
,点 的坐标为
的坐标为
(1)当 时,求
时,求 的坐标满足
的坐标满足 的概率。
的概率。
(2)当 时,求
时,求 的坐标满足
的坐标满足 的概率。
的概率。
 ,
,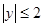 ,点
,点 的坐标为
的坐标为
(1)当
 时,求
时,求 的坐标满足
的坐标满足 的概率。
的概率。(2)当
 时,求
时,求 的坐标满足
的坐标满足 的概率。
的概率。(1)  的坐标满足
的坐标满足 的概率是
的概率是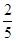 ;
;
(2) 的坐标满足
的坐标满足 的概率是
的概率是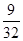 。
。
 的坐标满足
的坐标满足 的概率是
的概率是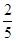 ;
;(2)
 的坐标满足
的坐标满足 的概率是
的概率是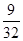 。
。本题主要考查几何概型中的面积类型和古典概型,两者最明显的区别是古典概型的基本事件是有限的,几何概型的基本事件是无限的。
(1)记“ 的坐标满足
的坐标满足 ”为事件
”为事件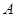 ,事件
,事件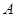 包含的基本事件有10种,所有的情况有当
包含的基本事件有10种,所有的情况有当 时,这是一个古典概型
时,这是一个古典概型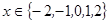 ,
,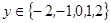
总的基本事件个数是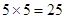 种,利用古典概型得到结论。
种,利用古典概型得到结论。
(2)因为x,y∈R,且围成面积,则为几何概型中的面积类型,先求区域为正方形ABCD的面积,然后得到记“ 的坐标满足
的坐标满足 ”为事件
”为事件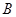
所构成的区域为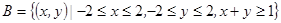 ,那么利用面积比得到结论。
,那么利用面积比得到结论。
解:由 得
得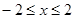 ,由
,由 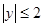 得
得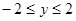 ,
,
(1)当 时,这是一个古典概型
时,这是一个古典概型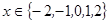 ,
,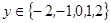 ………1分
………1分
总的基本事件个数是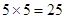 种。…………………………2分
种。…………………………2分
记“ 的坐标满足
的坐标满足 ”为事件
”为事件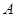 ……………………3分
……………………3分
事件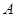 包含的基本事件有
包含的基本事件有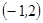 ,
,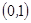 ,
,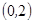 ,
,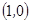 ,
,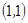 ,
,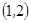 ,
,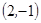
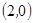 ,
,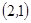 ,
,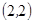 共10种。……………………………5分
共10种。……………………………5分
由古典概型的概率公式得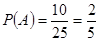 …………………………………6分
…………………………………6分
答: 的坐标满足
的坐标满足 的概率是
的概率是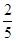 ………………………………7分
………………………………7分
(2)当 时,这是一个几何概型
时,这是一个几何概型
试验的全部结果构成的区域为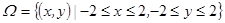 …………………8分
…………………8分
表示平面上的面积为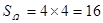 ……………………………9分
……………………………9分
记“ 的坐标满足
的坐标满足 ”为事件
”为事件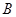 ……………………10分
……………………10分
所构成的区域为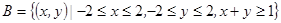 即下图阴影部分
即下图阴影部分
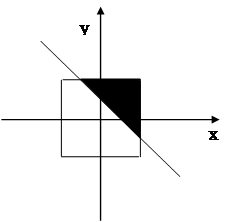
面积为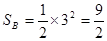 …………………………12分
…………………………12分
所以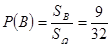 ………………………13分
………………………13分
答: 的坐标满足
的坐标满足 的概率是
的概率是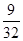 ………14分
………14分
(1)记“
 的坐标满足
的坐标满足 ”为事件
”为事件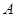 ,事件
,事件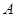 包含的基本事件有10种,所有的情况有当
包含的基本事件有10种,所有的情况有当 时,这是一个古典概型
时,这是一个古典概型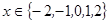 ,
,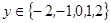
总的基本事件个数是
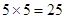 种,利用古典概型得到结论。
种,利用古典概型得到结论。(2)因为x,y∈R,且围成面积,则为几何概型中的面积类型,先求区域为正方形ABCD的面积,然后得到记“
 的坐标满足
的坐标满足 ”为事件
”为事件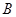
所构成的区域为
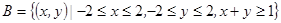 ,那么利用面积比得到结论。
,那么利用面积比得到结论。解:由
 得
得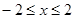 ,由
,由 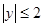 得
得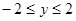 ,
, (1)当
 时,这是一个古典概型
时,这是一个古典概型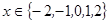 ,
,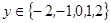 ………1分
………1分总的基本事件个数是
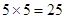 种。…………………………2分
种。…………………………2分记“
 的坐标满足
的坐标满足 ”为事件
”为事件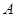 ……………………3分
……………………3分事件
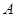 包含的基本事件有
包含的基本事件有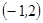 ,
,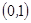 ,
,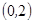 ,
,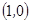 ,
,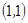 ,
,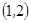 ,
,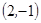
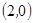 ,
,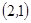 ,
,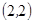 共10种。……………………………5分
共10种。……………………………5分由古典概型的概率公式得
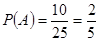 …………………………………6分
…………………………………6分答:
 的坐标满足
的坐标满足 的概率是
的概率是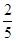 ………………………………7分
………………………………7分(2)当
 时,这是一个几何概型
时,这是一个几何概型试验的全部结果构成的区域为
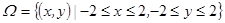 …………………8分
…………………8分表示平面上的面积为
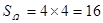 ……………………………9分
……………………………9分记“
 的坐标满足
的坐标满足 ”为事件
”为事件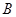 ……………………10分
……………………10分所构成的区域为
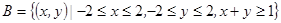 即下图阴影部分
即下图阴影部分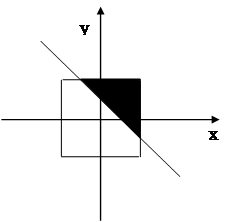
面积为
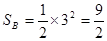 …………………………12分
…………………………12分所以
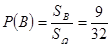 ………………………13分
………………………13分答:
 的坐标满足
的坐标满足 的概率是
的概率是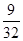 ………14分
………14分
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 ,
, ,已知
,已知 =
= ,
,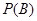 =
=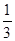 ,
, =
= ,则
,则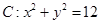 ,直线
,直线 ,圆C上任意一点A到直线
,圆C上任意一点A到直线 的距离小于2的概率为
的距离小于2的概率为

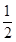
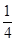
 ,集合
,集合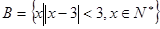 ,
,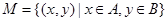
 所有可能的结果;
所有可能的结果;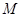 中任取一个元素,求“
中任取一个元素,求“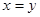 ”的概率
”的概率 ”的概率.
”的概率.



 ,那么掷两次一定会出现一次正面的情况
,那么掷两次一定会出现一次正面的情况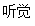 视觉
视觉 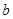
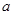
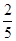 .
. 的样本,已知每位学生被抽到的概率都为
的样本,已知每位学生被抽到的概率都为 ,则
,则 ▲ .
▲ .