题目内容
在△ABC中,若N是AC上一点,且
=3
,点P在BN上,并满足
=
+m
,则实数m的值为( )
| CN |
| NA |
| AP |
| 3 |
| 11 |
| AB |
| AC |
分析:做出图形根据
,
共线和
=
-
,
=
-
的关系得出
,
,
的关系再根据
=3
可得出
,
,
的关系然后根据条件
=
+m
可得出对应系数相等即可求出m的值.
| BP |
| BN |
| BP |
| AP |
| AB |
| BN |
| AN |
| AB |
| AP |
| AB |
| AN |
| CN |
| NA |
| AP |
| AB |
| AC |
| AP |
| 3 |
| 11 |
| AB |
| AC |
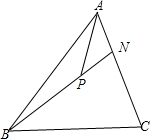
解答:解:(如图)∵
=3
∴
=4
∵
,
共线
∴由共线定理可得存在实数λ使得
=λ
∵
=
-
,
=
-
∴
-
=λ(
-
)
∴
=(1-λ)
+λ
又∵
=3
∴
=4
∵
=
+m
∴
=
+4m
∴
∴m=
故选D
| CN |
| NA |
∴
| AC |
| AN |
∵
| BP |
| BN |
∴由共线定理可得存在实数λ使得
| BP |
| BN |
∵
| BP |
| AP |
| AB |
| BN |
| AN |
| AB |
∴
| AP |
| AB |
| AN |
| AB |
∴
| AP |
| AB |
| AN |

又∵
| CN |
| NA |
∴
| AC |
| AN |
∵
| AP |
| 3 |
| 11 |
| AB |
| AC |
∴
| AP |
| 3 |
| 11 |
| AB |
| AN |
∴
|
∴m=
| 2 |
| 11 |
故选D
点评:本题主要考查了平面向量的基本定理,属难题.解题的关键是根据
,
共线和平面向量的基本定理得出
,
,
的关系(
=
+4m
)
| BP |
| BN |
| AP |
| AB |
| AC |
| AP |
| 3 |
| 11 |
| AB |
| AN |

练习册系列答案
相关题目
 ,点P在BN上,并满足
,点P在BN上,并满足 ,则实数m的值为( )
,则实数m的值为( )


