题目内容
(2013•昌平区一模)在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,那么(
-
)•
=
•
的取值范围是
| AB |
| AC |
| AD |
2
2
;若E是AB的中点,P是△ABC(包括边界)内任一点.则| AD |
| EP |
[-9,9]
[-9,9]
.分析:由条件可得
=
,故(
-
)•
=(
-
)•
=
,由此求得(
-
)•
的值.以CA所在的直线为x轴,以CB所在的直线为y轴,建立平面直角坐标系,利用简单的线性规划求得t=
•
的取值范围.
| AD |
| ||||
| 2 |
| AB |
| AC |
| AD |
| AB |
| AC |
| ||||
| 2 |
| ||||
| 2 |
| AB |
| AC |
| AD |
| AD |
| EP |
解答:解:∵在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,那么
=
,
2=
2+
2=16+4=20.
∴(
-
)•
=(
-
)•
=
=
=2.
以CA所在的直线为x轴,以CB所在的直线为y轴,建立平面直角坐标系,则A的坐标为(4,0),B的坐标为(0,2),
由线段的中点公式可得点D的坐标为(0,1),点E的坐标为(2,1),设点P的坐标为(x,y),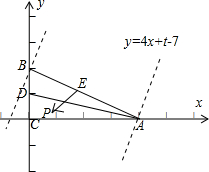
则由题意可得可行域为△ABC及其内部区域,故有
.
令t=
•
=(-4,1)•(x-2,y-1)=7-4x+y,即 y=4x+t-7.
故当直线y=4x+t-7过点A(4,0)时,t取得最小值为7-16+0=-9,
当直线y=4x+t-7过点B(0,2)时,t取得最大值为 7-0+2=9,
故t=
•
的取值范围是[-9,9],
故答案为 2,[-9,9].
| AD |
| ||||
| 2 |
| AB |
| AC |
| BC |
∴(
| AB |
| AC |
| AD |
| AB |
| AC |
| ||||
| 2 |
| ||||
| 2 |
| 20-16 |
| 2 |
以CA所在的直线为x轴,以CB所在的直线为y轴,建立平面直角坐标系,则A的坐标为(4,0),B的坐标为(0,2),
由线段的中点公式可得点D的坐标为(0,1),点E的坐标为(2,1),设点P的坐标为(x,y),
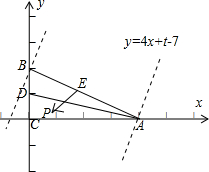
则由题意可得可行域为△ABC及其内部区域,故有
|
令t=
| AD |
| EP |
故当直线y=4x+t-7过点A(4,0)时,t取得最小值为7-16+0=-9,
当直线y=4x+t-7过点B(0,2)时,t取得最大值为 7-0+2=9,
故t=
| AD |
| EP |
故答案为 2,[-9,9].
点评:本题主要考查两个向量的数量积运算,线段的中点公式,简单的线性规划问题,属于中档题.

练习册系列答案
相关题目
 (2013•昌平区一模)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图:
(2013•昌平区一模)为了解甲、乙两厂的产品的质量,从两厂生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: