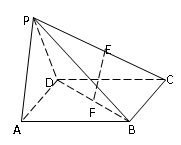
题目内容
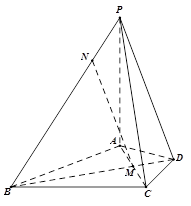
在四棱锥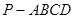 中,
中,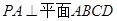 ,
,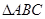 是正三角形,
是正三角形,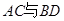 的交点
的交点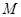 恰好是
恰好是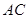 中点,又
中点,又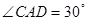 ,
,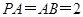 ,点
,点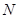 在线段
在线段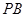 上,且
上,且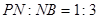 .
.
(1)求证: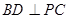 ;
;
(2)求证: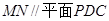 ;
;
(1)先证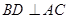 ,再证
,再证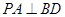 ,进而用线面垂直的判定定理即可证明;
,进而用线面垂直的判定定理即可证明;
(2)证明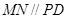 ,然后利用线面平行的判定定理即可证明.
,然后利用线面平行的判定定理即可证明.
解析试题分析:(1) 因为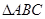 是正三角形,
是正三角形, 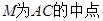 ,
, 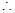
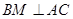 ,即
,即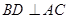
又因为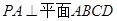 ,所以
,所以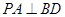
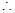
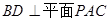
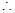
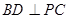
(2)在正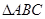 中,
中,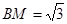
在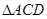 中,因为
中,因为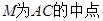 ,
,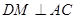 ,所以
,所以
又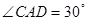 ,所以
,所以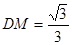 ,所以
,所以
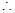
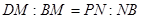 ,
,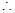
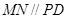
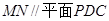
考点:本小题主要考查线面垂直和线面平行的证明.
点评:要证明线面垂直和线面平行,就要紧扣相应的判定定理和性质定理,定理中要求的条件要一一列举出来,缺一不可.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
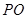 中,已知
中,已知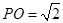 ,⊙O的直径
,⊙O的直径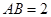 ,
,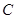 是
是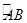 的中点,
的中点,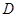 为
为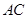 的中点.
的中点.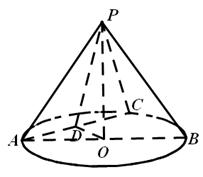
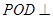 平面
平面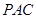 ;
;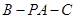 的余弦值.
的余弦值. 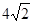 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。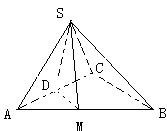
 的对棱
的对棱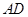 、
、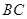 成
成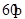 的角,且
的角,且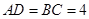 ,平行于
,平行于 、
、 、
、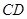 、
、 于
于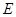 、
、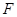 、
、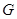 、
、 .
.
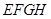 为平行四边形;
为平行四边形;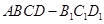 中,四边形
中,四边形 为菱形,
为菱形, ,
, ,面
,面 ∥面
∥面 、
、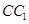 、
、 都垂直于面
都垂直于面 ,
, 为
为
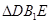 为等腰直角三角形;
为等腰直角三角形; ∥面
∥面 .
.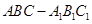 中,
中,

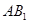 与
与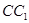 所成角的大小;
所成角的大小;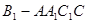 的体积。
的体积。 的底面是菱形,且
的底面是菱形,且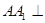 面
面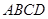 ,
,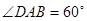 ,
,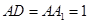 ,
, 为棱
为棱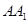 的中点,
的中点,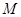 为线段
为线段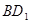 的中点,
的中点,
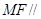 面
面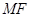 与平面
与平面 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;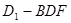 的体积.
的体积.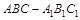 中,
中,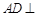 平面
平面 ,其垂足
,其垂足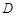 落在直线
落在直线 上.
上.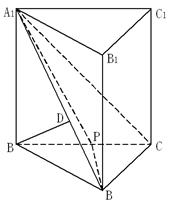
 ;
;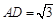 ,
,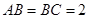 ,
,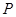 为
为 的中点,求三棱锥
的中点,求三棱锥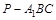 的体积.
的体积.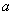 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=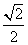 AD.
AD.