题目内容
(2012•宁德模拟)若直线kx-y-2=0与曲线
=x-1有两个不同的交点,则实数k的取值范围是( )
| 1-(y-1)2 |
分析:将直线化成斜截式,可得直线经过点(0,-2),将曲线方程化简整理,得该曲线是以(1,1)为圆心,半径为1的圆位于直线x=1右侧的部分.作出图形,观察直线的斜率k的变化,再结合计算即可得到实数k的取值范围.
解答:解:直线kx-y-2=0化成y=kx-2,可得它必定经过点(0,-2)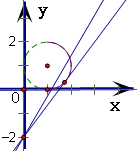
而曲线
=x-1,可变形整理为(x-1)2+(y-1)2=1(x≥1)
∴该曲线是以(1,1)为圆心,半径为1的圆位于直线x=1右侧的部分
设直线在圆下方与圆相切时的斜率为k1,直线过点(1,0)与圆有两个交点时的斜率为k2.
可得当直线kx-y-2=0与曲线有两个不同的交点时,斜率k满足k1<k≤k2.
由点(1,1)到直线kx-y-2=0的距离d=
=1,解得k1=
而k2=
=2,由此可得
<k≤2
故选A

而曲线
| 1-(y-1)2 |
∴该曲线是以(1,1)为圆心,半径为1的圆位于直线x=1右侧的部分
设直线在圆下方与圆相切时的斜率为k1,直线过点(1,0)与圆有两个交点时的斜率为k2.
可得当直线kx-y-2=0与曲线有两个不同的交点时,斜率k满足k1<k≤k2.
由点(1,1)到直线kx-y-2=0的距离d=
| |k-1-2| | ||
|
| 4 |
| 3 |
而k2=
| -2-0 |
| 0-1 |
| 4 |
| 3 |
故选A
点评:本题给出动直线与半圆有两个不同的交点,求直线斜率k的取值范围,着重考查了曲线与方程的化简和直线与圆的位置关系等知识,属于基础题.

练习册系列答案
相关题目
 (2012•宁德模拟)一空间几何体的三视图如图所示,则该几何体的体积为
(2012•宁德模拟)一空间几何体的三视图如图所示,则该几何体的体积为 (2012•宁德模拟)如图所示,在矩形ABCD中,AB=3
(2012•宁德模拟)如图所示,在矩形ABCD中,AB=3