题目内容
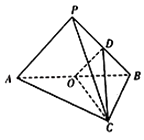
【题目】如图,三棱柱ABC﹣A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1 , AC的中点. 
(1)在平面ABC内过点A作AM∥平面PQB1交BC于点M,并写出作图步骤,但不要求证明;
(2)若侧面ACC1A1⊥侧面ABB1A1 , 求直线A1C1与平面PQB1所成角的正弦值.
【答案】
(1)解:取BC中点M,连接AM,则AM∥平面PQB1;
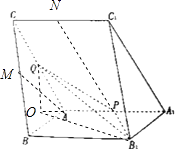
(2)解:作QO⊥平面ABB1A1,与A1A延长线交于O,则AO=1,QO= ![]() ,
,
OB1= ![]() =
= ![]() ,∴QB1=
,∴QB1= ![]() ,
,
∵B1P=2,PQ=2 ![]() ,
,
∴cos∠QPB1= ![]() =﹣
=﹣ ![]() ,
,
∴sin∠QPB1= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
作PN∥C1A1,则直线A1C1与平面PQB1所成角=直线PN与平面PQB1所成角,
∵ ![]() =2
=2 ![]() ,∴
,∴ ![]() =
= ![]() =2,
=2,
设N到平面PQB1的距离为h,则 ![]() ,∴h=
,∴h= ![]() ,
,
∴直线A1C1与平面PQB1所成角的正弦值= ![]() =
= ![]() .
.

【解析】(1)取BC中点M,连接AM,则AM∥平面PQB1;(2)作PN∥C1A1,则直线A1C1与平面PQB1所成角=直线PN与平面PQB1所成角,求出N到平面PQB1的距离,即可求直线A1C1与平面PQB1所成角的正弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目