题目内容
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
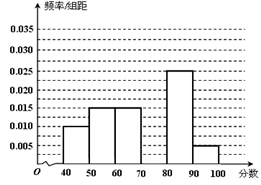
(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.

(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
(1)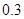 ,频率分布直方图见解析;(2)
,频率分布直方图见解析;(2)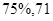 ;(3)
;(3)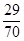 。
。
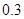 ,频率分布直方图见解析;(2)
,频率分布直方图见解析;(2)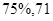 ;(3)
;(3)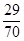 。
。试题分析:(1)频率分布直方图中,每个小矩形的面积即为每组的频率,所有小矩形面积之和为
 ,故成
,故成绩落在[70,80)上的频率为
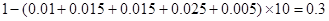 ,(2)这次考试的及格
,(2)这次考试的及格 率为成绩落在[60,100)上的频率,(3)成绩在[70,80)、[80,90)、[90,100]的人数分别为
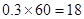 ,
,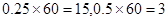 ,每个学生被选取的机会均等,即为古典概型,基本事件总数为
,每个学生被选取的机会均等,即为古典概型,基本事件总数为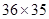 ,两人同一分数段包括的基本事件个数为
,两人同一分数段包括的基本事件个数为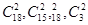 ,然后用古典概型公式求解。
,然后用古典概型公式求解。(1)成绩落在[70,80)上的频率是
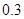 ,频率分布直方图如下图
,频率分布直方图如下图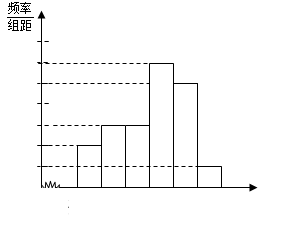
(2) 估计这次考试的及格率(60分及以上为及格)为1-0.01×10-0.015×10=75﹪
平均分:45×
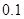 +55×0.15+65×0.15+75×
+55×0.15+65×0.15+75×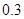 +85×0.25+95×
+85×0.25+95×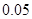 =71----8分
=71----8分(3) 成绩是70分以上(包括70分)的学生人数为(
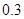 +0.025+
+0.025+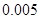 )×10×60=36
)×10×60=36所以所求的概率为
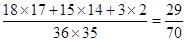 12分
12分 频数/样本容量的应用;(2)频率分布直方图中,每个小矩形的面积即为每组的频率,所有小矩形面积之和为
频数/样本容量的应用;(2)频率分布直方图中,每个小矩形的面积即为每组的频率,所有小矩形面积之和为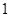 ,(3)古典概型的定义及其概率的求法。
,(3)古典概型的定义及其概率的求法。
练习册系列答案
相关题目
 (元)
(元)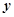 (件)
(件)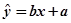 中的
中的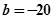 ,据此模型预报单价为10元时的销量为多少件?
,据此模型预报单价为10元时的销量为多少件?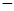 成本)
成本)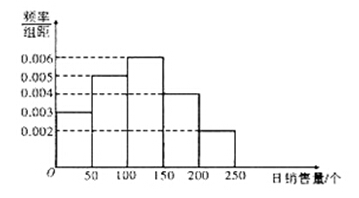
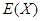 及方差
及方差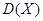 .
. (件)与销售价格
(件)与销售价格 (元/件)负相关,则其回归方程可能是( )
(元/件)负相关,则其回归方程可能是( )



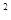 ≥6.635)=0.010,故我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病
≥6.635)=0.010,故我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表: 人中随机抽取1人抽到喜爱打篮球的学生的概率为
人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
. ,其中
,其中 )
)