题目内容
已知向量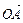 (
( cos
cos ,
,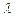 sin
sin ) (
) ( ≠0 ),
≠0 ),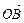 =" (" – sin
=" (" – sin ,cos
,cos ),其中O为坐标原点。(1)若
),其中O为坐标原点。(1)若 =
= –
– 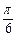 ,求向量
,求向量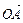 与
与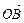 的夹角;(2)若|
的夹角;(2)若|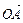 |≥2|
|≥2|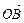 |对任意实数
|对任意实数 、
、 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。
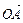 (
( cos
cos ,
,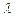 sin
sin ) (
) ( ≠0 ),
≠0 ),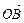 =" (" – sin
=" (" – sin ,cos
,cos ),其中O为坐标原点。(1)若
),其中O为坐标原点。(1)若 =
= –
– 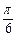 ,求向量
,求向量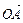 与
与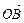 的夹角;(2)若|
的夹角;(2)若|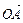 |≥2|
|≥2|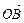 |对任意实数
|对任意实数 、
、 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。(1)故当 >0时,向量
>0时,向量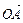 与
与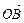 的夹角为
的夹角为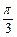 ;当
;当 <0时,向量
<0时,向量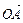 与
与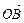 的夹角为
的夹角为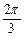 。(2)实数
。(2)实数 的取值范围是
的取值范围是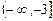 ∪
∪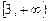 。
。
 >0时,向量
>0时,向量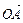 与
与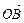 的夹角为
的夹角为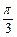 ;当
;当 <0时,向量
<0时,向量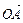 与
与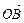 的夹角为
的夹角为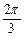 。(2)实数
。(2)实数 的取值范围是
的取值范围是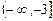 ∪
∪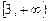 。
。(1)设向量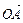 与
与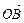 的夹角
的夹角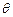 ,
,
则cos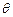 =
=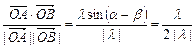 ,
,
当 >0时,cos
>0时,cos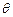 =
=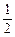 ,
,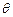 =
=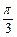 ;
;
当 <0时,cos
<0时,cos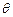 = –
= –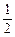 ,
, 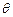 =
=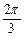 。
。
故当 >0时,向量
>0时,向量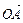 与
与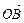 的夹角为
的夹角为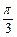 ;
;
当 <0时,向量
<0时,向量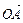 与
与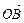 的夹角为
的夹角为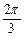 。
。
(2)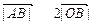 对任意的
对任意的 ,
, 恒成立, 即 (
恒成立, 即 ( cos
cos +sin
+sin )2 + (
)2 + ( sin
sin – cos
– cos )2≥4对任意的
)2≥4对任意的 ,
, 恒成立。
恒成立。
即 2 + 1 + 2
2 + 1 + 2 sin (
sin ( –
– ) ≥4对任意的
) ≥4对任意的 ,
, 恒成立,
恒成立,
所以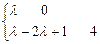 或
或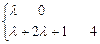 解得:
解得: ≥3或
≥3或 ≤ –3 。
≤ –3 。
故所求实数 的取值范围是
的取值范围是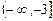 ∪
∪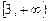 。
。
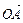 与
与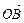 的夹角
的夹角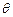 ,
,则cos
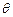 =
=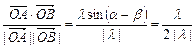 ,
,当
 >0时,cos
>0时,cos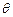 =
=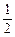 ,
,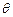 =
=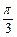 ;
;当
 <0时,cos
<0时,cos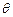 = –
= –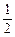 ,
, 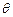 =
=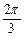 。
。故当
 >0时,向量
>0时,向量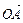 与
与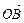 的夹角为
的夹角为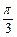 ;
;当
 <0时,向量
<0时,向量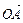 与
与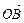 的夹角为
的夹角为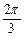 。
。
|
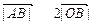 对任意的
对任意的 ,
, 恒成立, 即 (
恒成立, 即 ( cos
cos +sin
+sin )2 + (
)2 + ( sin
sin – cos
– cos )2≥4对任意的
)2≥4对任意的 ,
, 恒成立。
恒成立。即
 2 + 1 + 2
2 + 1 + 2 sin (
sin ( –
– ) ≥4对任意的
) ≥4对任意的 ,
, 恒成立,
恒成立,
|
|
|
|
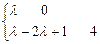 或
或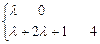 解得:
解得: ≥3或
≥3或 ≤ –3 。
≤ –3 。故所求实数
 的取值范围是
的取值范围是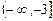 ∪
∪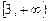 。
。
练习册系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为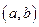 ,点
,点 的坐标为
的坐标为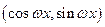 ,其中
,其中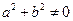 且
且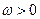 .设
.设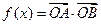 .
.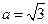 ,
,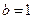 ,
,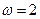 ,求方程
,求方程 在区间
在区间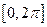 内的解集;
内的解集;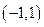 且法向量为
且法向量为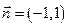 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数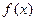 的值域为集合
的值域为集合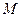 ,不等式
,不等式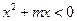 的解集为集合
的解集为集合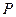 . 若
. 若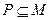 恒成立,求实数
恒成立,求实数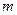 的最大值;
的最大值;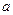 、
、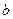 和
和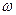 的值. 当
的值. 当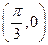 对称,且在
对称,且在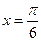 处
处


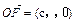 (c>0),
(c>0),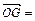 (n, n)(n∈R),
(n, n)(n∈R), 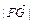 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:①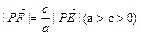 ,②
,②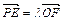 (其中
(其中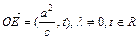 );③动点P的轨迹C经过点B(0,-1)。
);③动点P的轨迹C经过点B(0,-1)。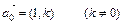 的直线l与曲线C交于不同两点M、N,若
的直线l与曲线C交于不同两点M、N,若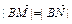 ,求k的取值范围。
,求k的取值范围。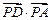 取最小值时,
取最小值时,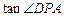 的值是
的值是



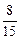
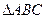 的边AB上任一点,E是边AC上任一点,连结DE,F是线段DE上一点,连结BF,设
的边AB上任一点,E是边AC上任一点,连结DE,F是线段DE上一点,连结BF,设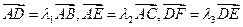 ,且
,且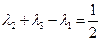 ,记
,记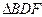 的面积为
的面积为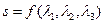 ,则S的最大值是
,则S的最大值是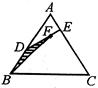
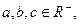 则
则 ,
, 时,取“
时,取“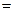 ”)】
”)】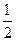
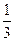
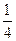
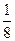
 值;
值; 的值
的值