��Ŀ����
�����Ӽ��Ĵ���ʹ���У�Ϊ���ҵ���ѵĴ��䷽������Ҫ�Ը��ֲ�ͬ�Ĵ��䷽ʽ���Ƚϣ�������ij��������Ʒ��ʱ����Ҫѡ�����ֲ�ͬ�����Ӽ������ڿɹ�ѡ�õIJ�ͬ���Ӽ���6�֣����з����Ϊ1�����Ӽ�1�֣������Ϊ2�����Ӽ�2�֣������Ϊ3�����Ӽ�3�֣������������ԭ����ͨ��Ҫ���ѡȡ���ֲ�ͬ�����Ӽ����д������飮��������ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3�ĸ��ʣ�
��������ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊż���ĸ��ʣ�
�����æα�ʾ��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮�ͣ�д���εķֲ��У�����ε���ѧ����E�Σ�
��������������һ���ȿ����¼��ĸ��ʣ����鷢���������¼��Ǵ�6�����Ӽ���ѡ���֣�����C62�ֽ���������������¼���ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3������C21�ֽ�������ݸ��ʹ�ʽ�õ������
��II���������Ӽ��ķ����֮��Ϊż�������ֿ��ܣ������Ϊ1��3�������Ϊ2��2�������Ϊ3��3������������ǻ���ģ����ݵȿ����¼��ĸ��ʺͻ����¼��ĸ��ʹ�ʽ�õ������
��III���α�ʾ��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮�ͣ���εĿ���ȡֵΪ3��4��5��6����ϱ�����Ӧ���¼�д���������ֵĸ��ʣ�д���ֲ��к�������
��II���������Ӽ��ķ����֮��Ϊż�������ֿ��ܣ������Ϊ1��3�������Ϊ2��2�������Ϊ3��3������������ǻ���ģ����ݵȿ����¼��ĸ��ʺͻ����¼��ĸ��ʹ�ʽ�õ������
��III���α�ʾ��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮�ͣ���εĿ���ȡֵΪ3��4��5��6����ϱ�����Ӧ���¼�д���������ֵĸ��ʣ�д���ֲ��к�������
����⣺����������֪������һ���ȿ����¼��ĸ��ʣ�
���鷢���������¼��Ǵ�6�����Ӽ���ѡ���֣�����C62�ֽ����
�����������¼���ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3������C21�ֽ����
�衰��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3��Ϊ�¼�A��
��P(A)=
=
��
����ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3�ĸ�����
��
�����衰��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊż����Ϊ�¼�B��
�������Ӽ��ķ����֮��Ϊż�������ֿ��ܣ������Ϊ1��3�������Ϊ2��2�������Ϊ3��3��
���з����Ϊ1��3�ĸ���Ϊ
=
��
�����Ϊ2��2�ĸ���Ϊ
=
��
�����Ϊ3��3�ĸ���Ϊ
=
��
��P(B)=
+
+
=
��
����ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊż���ĸ�����
��
���εĿ���ȡֵΪ3��4��5��6��
��P(��=3)=
=
��
P(��=4)=
=
��
P(��=5)=
=
��
P(��=6)=
=
��
��εķֲ���Ϊ
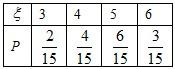
��E��=3��
+4��
+5��
+6��
=
��
���鷢���������¼��Ǵ�6�����Ӽ���ѡ���֣�����C62�ֽ����
�����������¼���ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3������C21�ֽ����
�衰��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3��Ϊ�¼�A��
��P(A)=
| ||
|
| 2 |
| 15 |
����ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊ3�ĸ�����
| 2 |
| 15 |
�����衰��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊż����Ϊ�¼�B��
�������Ӽ��ķ����֮��Ϊż�������ֿ��ܣ������Ϊ1��3�������Ϊ2��2�������Ϊ3��3��
���з����Ϊ1��3�ĸ���Ϊ
| ||
|
| 3 |
| 15 |
�����Ϊ2��2�ĸ���Ϊ
| ||
|
| 1 |
| 15 |
�����Ϊ3��3�ĸ���Ϊ
| ||
|
| 3 |
| 15 |
��P(B)=
| 3 |
| 15 |
| 1 |
| 15 |
| 3 |
| 15 |
| 7 |
| 15 |
����ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮��Ϊż���ĸ�����
| 7 |
| 15 |
���εĿ���ȡֵΪ3��4��5��6��
��P(��=3)=
| ||
|
| 2 |
| 15 |
P(��=4)=
| ||||
|
| 4 |
| 15 |
P(��=5)=
| ||||
|
| 6 |
| 15 |
P(��=6)=
| ||
|
| 3 |
| 15 |
��εķֲ���Ϊ

��E��=3��
| 2 |
| 15 |
| 4 |
| 15 |
| 6 |
| 15 |
| 3 |
| 15 |
| 14 |
| 3 |
���������⿼����ɢ����������ķֲ��к�����������ȿ����¼��ĸ��ʣ���һ�����͵����⣬������Ŀ�Ǹ߿�ÿһ��ؿ��ģ�

��ϰ��ϵ�д�
�����Ŀ
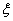 ��ʾ��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮�͡�
��ʾ��ѡ�õ����ֲ�ͬ�����Ӽ��ķ����֮�͡�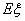 ����Ҫ��д��������̻�˵��������
����Ҫ��д��������̻�˵��������