题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 的图象上存在不同的两点
的图象上存在不同的两点![]() ,使得直线
,使得直线![]() 的斜率
的斜率![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时, ![]() 的减区间是
的减区间是![]() ,无增区间,当
,无增区间,当![]() 时,
时, ![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() ,当
,当![]() 时,
时, ![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() .
.
(Ⅱ)![]() 。
。
【解析】试题分析:(Ⅰ)先求函数![]() 的导数,再对参数
的导数,再对参数![]() 进行分类讨论,分别确定其单调性并求出其单调区间,(Ⅱ)先运用斜率公式将不等式等价转化为
进行分类讨论,分别确定其单调性并求出其单调区间,(Ⅱ)先运用斜率公式将不等式等价转化为![]() ,进而转化为不等式
,进而转化为不等式![]() 恒成立,然后构造函数
恒成立,然后构造函数![]() ,借助导数及其单调性建立不等式
,借助导数及其单调性建立不等式![]() 进行求解:
进行求解:
解:(Ⅰ) ![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时, ![]()
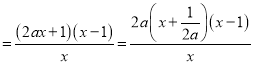 ,
,
(ⅰ)若![]() ,即
,即![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上是减函数;
上是减函数;
(ⅱ)若![]() ,即
,即![]() 时,
时, ![]() 时
时![]() ,
, ![]() 是增函数,
是增函数,
![]() 时,
时, ![]() ,
, ![]() 是减函数,
是减函数,
![]() 时,
时, ![]() ,
, ![]() 是减函数;
是减函数;
(ⅲ)若![]() ,即
,即![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 是增函数,
是增函数,
![]() 时,
时, ![]() ,
, ![]() 是减函数,
是减函数,
![]() 时,
时, ![]() ,
, ![]() 是减函数;
是减函数;
综上可得,当![]() 时,
时, ![]() 的减区间是
的减区间是![]() ,无增区间,
,无增区间,
当![]() 时,
时, ![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() ,
,
当![]() 时,
时, ![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() .
.
(Ⅱ)假设![]() 的图象上不存在两点
的图象上不存在两点![]() ,使得直线
,使得直线![]() 的斜率
的斜率![]() 成立,
成立,
则对![]() 的图象上任意两点
的图象上任意两点![]() ,都有
,都有![]() 成立,
成立,
即![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() ,
,
所以![]() 是减函数,
是减函数, ![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() .
.
即若对![]() 的图象上任意两点
的图象上任意两点![]() ,都有
,都有![]() 成立,则
成立,则![]() ,
,
所以若![]() 的图象上不存在两点
的图象上不存在两点![]() ,使得直线
,使得直线![]() 的斜率
的斜率![]() 成立,
成立,
则![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.