题目内容
【题目】如图,一辆汽车从A市出发沿海岸一条笔直公路以![]() 的速度向东匀速行驶,汽车开动时,在A市南偏东方向距A市500km且与海岸距离为300km的海上B处有一艘快艇与汽车同时出发,要把一份文件交给这辆汽车的司机.
的速度向东匀速行驶,汽车开动时,在A市南偏东方向距A市500km且与海岸距离为300km的海上B处有一艘快艇与汽车同时出发,要把一份文件交给这辆汽车的司机.
(1)快艇至少以多大的速度行驶才能把文件送到司机手中?
(2)求快艇以最小速度行驶时的行驶方向与![]() 所成角的大小.
所成角的大小.
(3)若快艇每小时最快行驶![]() ,快艇应如何行驶才能尽快把文件交到司机手中?最快需多长时间?
,快艇应如何行驶才能尽快把文件交到司机手中?最快需多长时间?

【答案】(1)快艇至少以![]() 的速度行驶才能把文件送到司机手中;(2)快艇以最小速度行驶时的行驶方向与
的速度行驶才能把文件送到司机手中;(2)快艇以最小速度行驶时的行驶方向与![]() 所成的角为90°;(3)快艇应垂直于海岸向北行驶才能尽快把文件交到司机手中,最快需要4h.
所成的角为90°;(3)快艇应垂直于海岸向北行驶才能尽快把文件交到司机手中,最快需要4h.
【解析】
(1)画图分析,设![]() 后与汽车在C处相遇,再根据三角形中的关系分别表示快艇与汽车所经过的路程,再化简求得快艇速度
后与汽车在C处相遇,再根据三角形中的关系分别表示快艇与汽车所经过的路程,再化简求得快艇速度![]() 与时间
与时间![]() 之间的函数关系,再利用二次不等式的最值分析即可.
之间的函数关系,再利用二次不等式的最值分析即可.
(2)根据(1)中的结论分析可得汽车与快艇路程构成的三角形中的边的关系,进而求得时间即可.
(3)设快艇以![]() 的速度沿
的速度沿![]() 行驶,
行驶,![]() 后与汽车在E处相遇,同(1)中的方法求得三角形各边的关系分析即可.
后与汽车在E处相遇,同(1)中的方法求得三角形各边的关系分析即可.
(1)如图所示,设快艇以![]() 的速度从B处出发,沿
的速度从B处出发,沿![]() 方向行驶,
方向行驶,![]() 后与汽车在C处相遇.
后与汽车在C处相遇.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的高,
边上的高,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
由余弦定理,得![]() ,
,
即![]() ,
,
整理得![]()
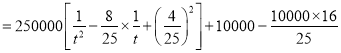
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,∴
,∴![]() .
.
即快艇至少以![]() 的速度行驶才能把文件送到司机手中.
的速度行驶才能把文件送到司机手中.
(2)由(1)可知,当![]() 时,在
时,在![]() 中,
中,
![]() ,
,![]() ,
,![]() ,由余弦定理,得
,由余弦定理,得![]() ,∴
,∴![]() .
.
故快艇以最小速度行驶时的行驶方向与![]() 所成的角为90°.
所成的角为90°.
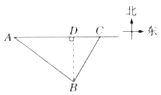
(3)如图所示,设快艇以![]() 的速度沿
的速度沿![]() 行驶,
行驶,![]() 后与汽车在E处相遇.
后与汽车在E处相遇.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
由余弦定理,得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
∵当![]() 时,
时,![]() ,
,![]() ,
,![]() ,∴快艇应垂直于海岸向北行驶才能尽快把文件交到司机手中,最快需要4h.
,∴快艇应垂直于海岸向北行驶才能尽快把文件交到司机手中,最快需要4h.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目