题目内容
【题目】设椭圆中心在坐标原点,焦点在x轴上,一个顶点坐标为(2,0),离心率为 ![]() .
.
(1)求这个椭圆的方程;
(2)若这个椭圆左焦点为F1 , 右焦点为F2 , 过F1且斜率为1的直线交椭圆于A、B两点,求△ABF2的面积.
【答案】
(1)解:设椭圆的方程为 ![]() ,
,
由题意,a=2, ![]() =
= ![]() ,∴c=
,∴c= ![]() ,b=1,
,b=1,
∴椭圆的方程为 ![]()
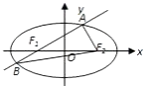
(2)解:左焦点F1(﹣ ![]() ,0),右焦点F2(
,0),右焦点F2( ![]() ,0),设A(x1,y1 ),
,0),设A(x1,y1 ),
B(x2,y2),
则直线AB的方程为 y=x+ ![]() .
.
由 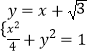 ,消x得 5y2﹣2
,消x得 5y2﹣2 ![]() y﹣1=0.∴y1+y2=
y﹣1=0.∴y1+y2= ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
∴|y1﹣y2|= ![]() =
= ![]() .
.
∴S△ABF2= ![]() +
+ ![]() =
= ![]() +
+ ![]()
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)设椭圆的方程为 ![]() ,有条件求得a 和c,从而求得b,进而得到椭圆的方程.(2)把直线AB的方程 代入椭圆的方程化简,利用根与系数的关系,求出|y1﹣y2|的值,利用S△ABF2=
,有条件求得a 和c,从而求得b,进而得到椭圆的方程.(2)把直线AB的方程 代入椭圆的方程化简,利用根与系数的关系,求出|y1﹣y2|的值,利用S△ABF2= ![]() +
+ ![]() =
= ![]() +
+ ![]() 求得结果.
求得结果.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目