题目内容
若函数 ,则对于不同的实数a,函数
,则对于不同的实数a,函数 的单调区间个数不可能是( )
的单调区间个数不可能是( )
| A.1个 | B.2个 | C.3个 | D.5个 |
B
解析试题分析:最高次项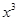 递增,无论a如何取值,当x---> +∞时,f(x)递增;
递增,无论a如何取值,当x---> +∞时,f(x)递增;
当x从左边-∞开始(当然没有开始)时, f(x)递增。
由于曲线是连续的,所以,(1)若中间连续递增,(a=0时)单调区间个数为1;
(2) 若中间只有一段递减,即增,减,增单调区间个数为3;
(3)若中间有2段递减,即增,减,增,减,增单调区间个数为5;
总之单调区间个数不可能为2。
另,无论x取何值,a取何值,原函数被分成三部分讨论(-∞,-1),[-1,1],(1,+∞).当a=0时,是一个单调区间,a不等于零时,三次函数,则不可能有两个单调区间 ,故选B 。
考点:函数的图象,应用导数研究函数的单调性。
点评:中档题,作为选择题,在解答过程中,可借助于就的函数的单调性,做出定性分析,简化解答过程。本题为选择题,不必“小题大作”。

练习册系列答案
相关题目
把函数 的图像向左平移
的图像向左平移 个单位,所得曲线的一部分
个单位,所得曲线的一部分
如图示,则 的值分别为
的值分别为
A. | B. | C. | D. |
下列函数在其定义域内,既是奇函数又存在零点的是( )
A. | B. |
C. | D.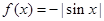 |
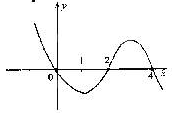
已知函数 ,其导函数
,其导函数 的图象如图所示,则
的图象如图所示,则 ( )
( )
| A.在(-∞,0)上为减函数 | B.在 0处取极小值 0处取极小值 |
| C.在(4,+∞)上为减函数 | D.在 2处取极大值 2处取极大值 |
设 ,
, ,
, ,则
,则 的大小顺序是( )
的大小顺序是( )
A. | B. | C. | D.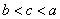 |
已知函数 ,若
,若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数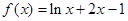 的零点所在区间为
的零点所在区间为
A.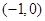 | B.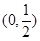 | C.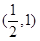 | D. |
 的图象大致是
的图象大致是
 对于区间D内任意的
对于区间D内任意的 ,有
,有

 成立,称
成立,称 在区间
在区间 上是 “凸函数”,则在△
上是 “凸函数”,则在△ 中,
中, 的最大值是( )
的最大值是( )


