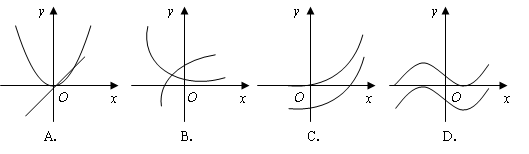
题目内容
在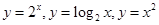 ,这三个函数中,当
,这三个函数中,当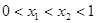 时,
时,
使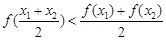 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A. 个 个 | B. 个 个 | C.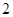 个 个 | D.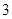 个 个 |
C
解析试题分析:根据题意,由于指数函数和对数函数底数大于1,因此是递增函数,而抛物线在给定区间是递增的,那么结合函数凹函数的特点可知,使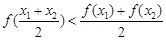 恒成立的函数为
恒成立的函数为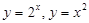 两个函数,故选C.
两个函数,故选C.
考点:函数的单调性
点评:本题考查指数函数的单调性、基本不等式比较数的大小.

练习册系列答案
相关题目
函数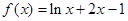 的零点所在区间为
的零点所在区间为
A.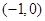 | B.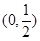 | C.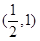 | D. |
已知 为定义在
为定义在 上的可导函数,且
上的可导函数,且
 对于任意
对于任意 恒成立,则( )
恒成立,则( )
A. , , |
B. , , |
C. , , |
D. , , |
函数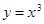 ( )
( )
A.是奇函数,且在 上是单调增函数 上是单调增函数 |
B.是奇函数,且在 上是单调减函数 上是单调减函数 |
C.是偶函数,且在 上是单调增函数 上是单调增函数 |
D.是偶函数,且在 上是单调减函数 上是单调减函数 |
把函数 的图像向左平移
的图像向左平移 个单位,所得图像的解析式是( )
个单位,所得图像的解析式是( )
A. | B. |
C. | D. |
定义在R上的函数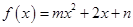 的值域是
的值域是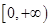 ,又对满足前面要求的任意实数
,又对满足前面要求的任意实数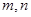 都有不等式
都有不等式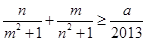 恒成立,则实数
恒成立,则实数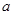 的最大值为
的最大值为
| A. 2013 | B. 1 | C. | D.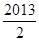 |
若 ,则
,则 的大小关系
的大小关系
A. | B. |
C. | D. |
 对于区间D内任意的
对于区间D内任意的 ,有
,有

 成立,称
成立,称 在区间
在区间 上是 “凸函数”,则在△
上是 “凸函数”,则在△ 中,
中, 的最大值是( )
的最大值是( )



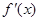 是函数
是函数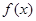 的导函数,将
的导函数,将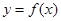 和
和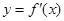 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )