题目内容
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如下:
分组(岁) | 频数 |
[25,30) | x |
[30,35) | y |
[35,40) | 35 |
[40,45) | 30 |
[45,50] | 10 |
合计 | 100 |
(Ⅰ)求频率分布表中x、y的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人重随机抽取2人各赠送精美礼品一份,设这2名市民中年龄在[35,40)内的人数为X,求X的分布列及数学期望.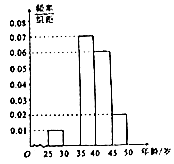
【答案】解:(I)由图知,P(25≤x<30)=0.01×5=0.05,故x=100×0.05=5; P(30≤x<35)=1﹣(0.05+0.35+0.3+0.1)=1﹣0.8=0.2
故y=100×0.2=20,
其 ![]() =
= ![]() =0.04
=0.04
(II)∵各层之间的比为5:20:35:30:10=1:4:7:6:2,且共抽取20人,
∴年龄在[35,40)内层抽取的人数为7人.
X可取0,1,2,P(X=k)= ![]() ,可得P(X=0)=
,可得P(X=0)= ![]() ,P(X=1)=
,P(X=1)= ![]() ,P(X=2)=
,P(X=2)= ![]() .
.
故X的分布列为:
X | 0 | 1 | 2 |
P | | | |
故E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =
= ![]() .
.
【解析】(I)利用频率分布直方图的性质即可得出.(II)各层之间的比为5:20:35:30:10=1:4:7:6:2,且共抽取20人,可得年龄在[35,40)内层抽取的人数为7人.X可取0,1,2,P(X=k)= ![]() ,即可得出.
,即可得出.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息,以及对离散型随机变量及其分布列的理解,了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 阅读快车系列答案
阅读快车系列答案