题目内容
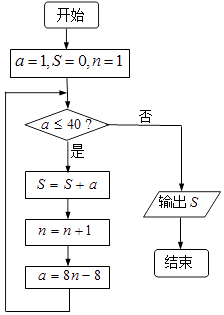
【题目】已知数列{an}的前n项和为Sn ， 满足 
，且a1=3． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证： 
．
【答案】解：（Ⅰ）数列{an}的前n项和为Sn ， 且 
， ∴Sn﹣Sn﹣1=2an﹣1+1，（n≥2，n∈N*），
即an=2an﹣1+1（n≥2，n∈N*），
∴an+1=2（an﹣1+1），
∴数列{an+1}是等比数列；
又a1+1=3+1=4，
∴ 
，
∴ 
；
（Ⅱ）由（Ⅰ）知， 
，
∴{ 
}是首项为 
，公比为 
的等比数列，
因此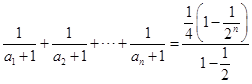 
= 
．
【解析】（Ⅰ）由数列{an}的前n项和与通项公式的定义，得出an=2an﹣1+1（n≥2，n∈N*），从而得出数列{an+1}是等比数列，由此求出{an}的通项公式；（Ⅱ）由（Ⅰ）写出数列{an+1}的通项公式，从而得出{ 
}是等比数列，求出其前n项和，即可证明不等式成立．
【考点精析】根据题目的已知条件，利用数列的通项公式的相关知识可以得到问题的答案，需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
【题目】某手机卖场对市民进行国产手机认可度的调查，随机抽取100名市民，按年龄（单位：岁）进行统计的频数分布表和频率分布直方图如下：
分组（岁） | 频数 |
[25，30） | x |
[30，35） | y |
[35，40） | 35 |
[40，45） | 30 |
[45，50] | 10 |
合计 | 100 |
（Ⅰ）求频率分布表中x、y的值，并补全频率分布直方图；
（Ⅱ）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加国产手机用户体验问卷调查，现从这20人重随机抽取2人各赠送精美礼品一份，设这2名市民中年龄在[35，40）内的人数为X，求X的分布列及数学期望．
