题目内容
已知α,β角的终边均在第一象限,则“α>β”是“sin α>sin β”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
D
当α>β时,令α=390°,β=60°,
则sin 390°=sin 30°=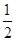 <sin 60°=
<sin 60°=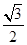 ,
,
故sinα>sinβ不成立;
当sinα>sinβ时,令α=60°,β=390°满足上式,
此时α<β,故“α>β”是“sin α>sin β”的既不充分也不必要条件,选D.
则sin 390°=sin 30°=
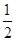 <sin 60°=
<sin 60°=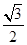 ,
,故sinα>sinβ不成立;
当sinα>sinβ时,令α=60°,β=390°满足上式,
此时α<β,故“α>β”是“sin α>sin β”的既不充分也不必要条件,选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
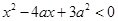 ,其中
,其中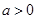 ,命题
,命题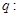 实数
实数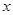 满足
满足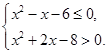 .
.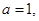 且
且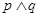 为真,求实数
为真,求实数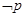 是
是
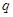 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.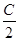
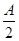 =
=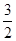 b.
b.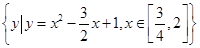 ,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.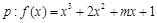 在(
在(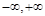 )上单调递增;
)上单调递增;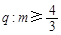 ,则p是q的( )
,则p是q的( )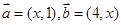 ,则“
,则“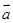 ∥
∥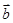 ”是“
”是“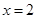 ”的
”的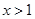 ”是“
”是“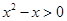 ”的 ( )
”的 ( )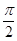 ”的
”的