题目内容

求函数y=
3
cosx
2+sinx
的值域
[-1，1]
[-1，1]
．
分析：由y=
3
cosx
2+sinx
转化为
y
3
=
cosx
2+sinx
，则
y
3
可看成单位圆上的动点（sinx，cosx）与点Q（-2，0）连线的斜率，借助于图形，即可得到y的范围．
解答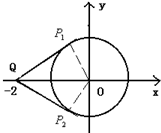：解：设点P（sinx，cosx），Q（-2，0），
则
y
3
可看成单位圆上的动点P与点Q连线的斜率，如右图：
设直线QP1是方程为y=k（x+2），即kx-y+2k=0，
则圆心（0，0）到它的距离d=
|2k|
k2+1
=1，
解得k1=-
3
3
或k2=
3
3
，
所以-
3
3
≤
y
3
≤
3
3
，即-1≤y≤1，
故答案为：[-1，1]．
点评：本题以三角函数为载体考查分式函数的值域，属于求三角函数的最值问题，属于基本题．
练习册系列答案
相关题目
已知向量
m
=(2sinx，2cosx)，
n
=(
3
cosx，cosx)，f(x)=
m
•
n
-1．
（1）求函数f（x）的最小正周期和单调递增区间；
（2）将函数y=f（x）的图象上各点的纵坐标保持不变，横坐标先缩短到原来的
1
2
，把所得到的图象再向左平移
π
6
单位，得到函数y=g（x）的图象，求函数y=g（x）在区间[0，
π
8
]上的最小值．
已知
m
=(2sinx，2cosx)，
n
=(
3
cosx，cosx)，f(x)=
m
•
n
-1
（1）求函数y=f（x）的最小正周期和单调递增区间；
（2）将函数y=f（x）的图象上各点的纵坐标保持不变，横坐标先缩短到原来的
1
3
，把所得到的图象再向右平移
π
12
单位，得到函数y=g（x）的图象，求函数y=g（x）在区间[0，
π
12
]上的最大值．
设函数f（x）=msinx+3cosx（x∈R），试分别解答下列两小题．
（ I）若函数f（x）的图象与直线y=n（n为常数）相邻两个交点的横坐标为x1=
π
12
，x2=
7π
12
，求函数y=f（x）的解析式，并写出函数f（x）的单调递增区间；
（ II）当m=
3
时，在△ABC中，满足f(A)=2
3
，且BC=1，若E为BC中点，试求AE的最大值．
（2012•威海一模）已知向量
m
=(2cosx，
3
cosx-sinx)，
n
=(sin(x+
π
6
)，sinx)，且满足f(x)=
m
•
n
．
（I）求函数y=f（x）的单调递增区间；
（II）设△ABC的内角A满足f（A）=2，且
AB
•
AC
=
3
，求边BC的最小值．
（2012•丰台区二模）已知函数f(x)=cosx(
3
cosx-sinx)-
3
．
（Ⅰ）求f(
π
3
)的值；
（Ⅱ）求函数y=f（x）在区间[0，
π
2
]上的最小值，并求使y=f（x）取得最小值时的x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网