题目内容
设函数f(x)=msinx+3cosx(x∈R),试分别解答下列两小题.
( I)若函数f(x)的图象与直线y=n(n为常数)相邻两个交点的横坐标为x1=
,x2=
,求函数y=f(x)的解析式,并写出函数f(x)的单调递增区间;
( II)当m=
时,在△ABC中,满足f(A)=2
,且BC=1,若E为BC中点,试求AE的最大值.
( I)若函数f(x)的图象与直线y=n(n为常数)相邻两个交点的横坐标为x1=
| π |
| 12 |
| 7π |
| 12 |
( II)当m=
| 3 |
| 3 |
分析:(I)根据函数图象与y=n相邻的两交点的横坐标的值列出关系式,表示出m,利用和差化积公式化简后,再利用特殊角的三角函数值变形,求出m的值,确定出函数f(x)的解析式,由f(x)的解析式提取-6,然后利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的图象与性质得到正弦函数的地增区间,列出关于x的不等式,求出不等式的解集得到x的范围,即为函数的递增区间;
(II)把m的值代入第一问化简得到的函数解析式中,根据f(A)=2
,利用特殊角的三角函数值计算后求出A的度数,构造一个圆,弦BC所对的圆周角为∠A,点A在弦BC所对的优弧上运动,且不与B与C重合,可得出当△ABC为等腰三角形,AB=AC,且AE过圆心O时,此时AE最大,由E为BC的中点,由∠A的度数,利用同弧所对的圆心角等于圆周角的2倍,求出∠BOC的度数,由OB=OC,得出三角形BOC为等边三角形,根据三线合一得到AE垂直于BC,在直角三角形OBE中,根据勾股定理求出OE的长,再由AO+OE即可求出此时AE的长,即为AE的最大值.
(II)把m的值代入第一问化简得到的函数解析式中,根据f(A)=2
| 3 |
解答:解:(I)根据题意得:
msin
+3cos
=msin
+3cos
=n,
变形得:m=
=
=3
,
∴f(x)=3
sinx+3cosx=6sin(x+
),
∵正弦函数的单调递增区间为[2kπ-
,2kπ+
](k∈Z),
∴令2kπ-
≤x+
≤2kπ+
(k∈Z),
解得:2kπ-
≤x≤2kπ+
(k∈Z),
则函数f(x)的递增区间为[2kπ-
,2kπ+
](k∈Z);
(II)把m=
代入解析式得:f(x)=
sinx+3cosx=2
sin(x+
),
∵f(A)=2
,∴2
sin(A+
)=2
,即sin(A+
)=1,
又A为三角形的内角,∴A+
=
,即A=
,又BC=1,
假设∠A为弦BC所对的圆周角,画出相应的图形,如图所示:
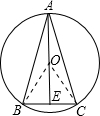
当△ABC为等腰三角形,AB=AC,且AE过圆心O时,此时AE最大,
∵∠BAC=30°,
∴∠BOC=60°,又OB=OC,且BC=1,
∴△BOC为边长为1的等边三角形,
又E为BC的中点,∴BE=CE=
BC=
,且OE⊥BC,
在直角三角形BOE中,根据勾股定理得:OE=
=
,
又OA=OB=1,∴AE=AO+OE=1+
,
则AE的最大值为1+
.
msin
| π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
| 7π |
| 12 |
变形得:m=
3(cos
| ||||
sin
|
-6sin
| ||||
-2cos
|
| 3 |
∴f(x)=3
| 3 |
| π |
| 6 |
∵正弦函数的单调递增区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
∴令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:2kπ-
| 2π |
| 3 |
| π |
| 3 |
则函数f(x)的递增区间为[2kπ-
| 2π |
| 3 |
| π |
| 3 |
(II)把m=
| 3 |
| 3 |
| 3 |
| π |
| 3 |
∵f(A)=2
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
又A为三角形的内角,∴A+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
假设∠A为弦BC所对的圆周角,画出相应的图形,如图所示:

当△ABC为等腰三角形,AB=AC,且AE过圆心O时,此时AE最大,
∵∠BAC=30°,
∴∠BOC=60°,又OB=OC,且BC=1,
∴△BOC为边长为1的等边三角形,
又E为BC的中点,∴BE=CE=
| 1 |
| 2 |
| 1 |
| 2 |
在直角三角形BOE中,根据勾股定理得:OE=
| OB2-BE2 |
| ||
| 2 |
又OA=OB=1,∴AE=AO+OE=1+
| ||
| 2 |
则AE的最大值为1+
| ||
| 2 |
点评:此题属于解三角形的题型,涉及的知识有:和差化积公式,两角和与差的正弦函数公式,正弦函数的单调性,等边三角形的判定与性质,等腰三角形的性质,圆周角定理,以及勾股定理,其中构造如图所示的图形,找出当△ABC为等腰三角形,AB=AC,且AE过圆心O时,此时AE最大是解本题第二问的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
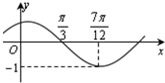 已知函数f(x)=Msin(ωx+φ)(其中
已知函数f(x)=Msin(ωx+φ)(其中