题目内容
【题目】已知函数f(x)=x2+mx﹣4在区间[﹣2,1]上的两个端点处取得最大值和最小值.
(1)求实数m的所有取值组成的集合A;
(2)试写出f(x)在区间[﹣2,1]上的最大值g(m);
(3)设h(x)=﹣ ![]() x+7,令F(m)=
x+7,令F(m)= ![]() ,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围.
,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围.
【答案】
(1)解:∵f(x)=x2+mx﹣4在区间[﹣2,1]上的两个端点处取得最大值和最小值,
∴函数在区间[﹣2,1]上是单调函数,
又∵函数f(x)的图象为开口向上的抛物线,对称轴为x=﹣ ![]()
∴必有﹣ ![]() ≥1,或﹣
≥1,或﹣ ![]() ≤﹣2,解得m≥4或 m≤﹣2,
≤﹣2,解得m≥4或 m≤﹣2,
∴实数m的所有取值组成的集合A={m|m≥4或 m≤﹣2}
(2)解:当 m≥4时,﹣ ![]() ≤﹣2,函数f(x)在区间[﹣2,1]上单调递增,
≤﹣2,函数f(x)在区间[﹣2,1]上单调递增,
∴函数f(x)的最大值g(m)=f(1)=m﹣3;
当m≤﹣2 时,﹣ ![]() ≥1,函数f(x)在区间[﹣2,1]上单调递减,
≥1,函数f(x)在区间[﹣2,1]上单调递减,
∴函数f(x)的最大值g(m)=f(﹣2)=﹣2m
(3)解:由题意可知F(m)= 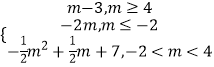 ,
,
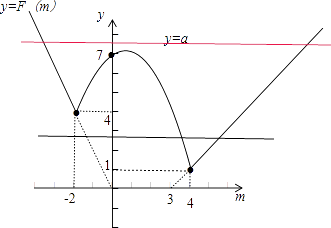
关于m的方程F(m)=a恰有两个不相等的实数根等价于y=F(m)的图象与y=a的图象有两个不同的交点,
作图可知实数a的取值范围为:a> ![]() 或1<a<4
或1<a<4
【解析】(1)问题等价于函数在区间[﹣2,1]上是单调函数,由二次函数可得﹣ ![]() ≥1,或﹣
≥1,或﹣ ![]() ≤﹣2,解得不等式即可;(2)分类讨论结合单调性可得:当 m≥4时g(m)=f(1)=m﹣3,当m≤﹣2时g(m)=f(﹣2)=﹣2m.(3)由题意可知F(m)=
≤﹣2,解得不等式即可;(2)分类讨论结合单调性可得:当 m≥4时g(m)=f(1)=m﹣3,当m≤﹣2时g(m)=f(﹣2)=﹣2m.(3)由题意可知F(m)= 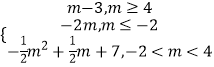 ,问题等价于y=F(m)的图象与y=a的图象有两个不同的交点,数形结合易得答案.
,问题等价于y=F(m)的图象与y=a的图象有两个不同的交点,数形结合易得答案.
【考点精析】通过灵活运用集合的补集运算和二次函数在闭区间上的最值,掌握对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 即可以解答此题.
即可以解答此题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案