题目内容
(2013•唐山一模)不等式组
,表示的平面区域的面积为
,则a=( )
|
| 15 |
| 2 |
分析:本题主要考查线性规划的基本知识,先画出约束条件
的可行域,根据已知条件中,表示的平面区域的面积等于
,构造关于a的方程,解方程即可得到答案.
|
| 15 |
| 2 |
解答: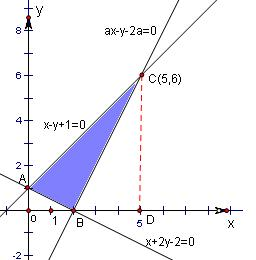 解:不等式组
解:不等式组
所围成的区域如图所示.
∵其面积为
,设C(m,m+1),
则SAODC-SABO-ABCD=S△ABC,
即
(1+m+1)m-
×1×2-
×(m-2)(m+1)=
解得m=5,
∴C的坐标为(5,6),
代入ax-y-2a=0,
得a=2.
故选C.
 解:不等式组
解:不等式组
|
∵其面积为
| 15 |
| 2 |
则SAODC-SABO-ABCD=S△ABC,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
解得m=5,
∴C的坐标为(5,6),
代入ax-y-2a=0,
得a=2.
故选C.
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 (2013•唐山一模)如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,∠APD=
(2013•唐山一模)如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,∠APD=