题目内容
从空间一点O出发的四条射线两两所成的角都是θ,则θ一定是
| A.锐角 | B.直角 | C.钝角 | D.锐角或钝角 |
C
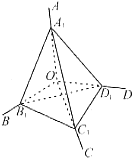
分析:如图,在射线OA、OB、OC、OD上分别截取OA1、OB1、OC1、OD1,使
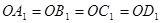 。由四条射线两两所成的角都是θ,得三棱锥
。由四条射线两两所成的角都是θ,得三棱锥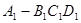 是正四面体,O是正四面体的中心。设
是正四面体,O是正四面体的中心。设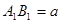 ,使用勾股定理及射影定理计算得
,使用勾股定理及射影定理计算得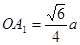 。
。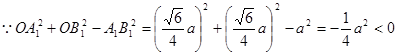
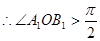
即θ为钝角。故选C。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
题目内容
| A.锐角 | B.直角 | C.钝角 | D.锐角或钝角 |

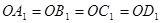 。由四条射线两两所成的角都是θ,得三棱锥
。由四条射线两两所成的角都是θ,得三棱锥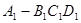 是正四面体,O是正四面体的中心。设
是正四面体,O是正四面体的中心。设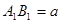 ,使用勾股定理及射影定理计算得
,使用勾股定理及射影定理计算得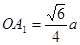 。
。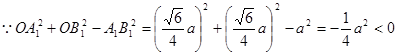
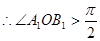

 口算题天天练系列答案
口算题天天练系列答案