Question

9粒种子分种在3个坑内，每坑3粒，每粒种子发芽的概率为0.5，若一个坑内至少有1粒种子发芽，则这个坑不需要补种；若一个坑内的种子都没发芽，则这个坑需要补种．假定每个坑至多补种一次，每补种1个坑需10元，用ξ表示补种费用，写出ξ的分布列并求ξ的数学期望．（精确到0.01）

Answer 1

【答案】分析：首先根据独立重复试验的概率公式计算出一个坑不需要补种的概率，由题意知一共种了3个坑，每个坑至多补种一次，每补种1个坑需10元，得到变量ξ的可能取值是0，10，20，30，根据独立重复试验得到概率的分布列．
解答：解：首先根据独立重复试验的概率公式计算出一个坑不需要补种的概率p=1-C₃³0.5³=0.875
由题意知一共种了3个坑，每个坑至多补种一次，每补种1个坑需10元
得到变量ξ的可能取值是0，10，20，30，
ξ=0，表示没有坑需要补种，
根据独立重复试验得到概率
P（ξ=0）=C₃³0.875³=0.670
P（ξ=10）=C₃²0.875²×0.125=0.287
P（ξ=20）=C₃¹×0.875×0.125²=0.041
P（ξ=30）=0.125³=0.002
∴变量的分布列是

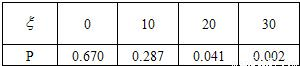
∴ξ的数学期望为：Eξ=0×0.670+10×0.287+20×0.041+30×0.002=3.75
点评：考查运用概率知识解决实际问题的能力，对立事件是指同一次试验中，不会同时发生的事件，遇到求用至少来表述的事件的概率时，往往先求它的对立事件的概率．