题目内容
下列给出函数f(x)与g(x)的各组中,是同一个关于x的函数的是
- A.
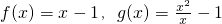
- B.
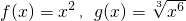
- C.f(x)=2x-1,g(x)=2x+1
- D.f(x)=1,g(x)=x0
B
分析:我们确定一个函数的三要素是:定义域、值域和对应法则,事实上只要两个函数的定义域和对应法则相同,值域也就随之而确定.据此可判断出两个函数是否是同一函数.
解答:A.函数f(x)=x-1的定义域是实数集R,而函数g(x)=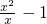 的定义域是{x|x≠0},故两个函数不是同一个函数.
的定义域是{x|x≠0},故两个函数不是同一个函数.
同理D中的两个函数的定义域也不同.故不是同一个函数.
C.中的对应法则不同,故不是同一个函数.
B.∵g(x)=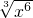 =x2,而f(x)=x2,∴函数f(x)与g(x)是同一个函数.
=x2,而f(x)=x2,∴函数f(x)与g(x)是同一个函数.
故选B.
点评:本题考查两个函数是否是同一个函数,据确定一个函数的三要素(定义域、值域和对应法则)不难判断出.
分析:我们确定一个函数的三要素是:定义域、值域和对应法则,事实上只要两个函数的定义域和对应法则相同,值域也就随之而确定.据此可判断出两个函数是否是同一函数.
解答:A.函数f(x)=x-1的定义域是实数集R,而函数g(x)=
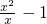 的定义域是{x|x≠0},故两个函数不是同一个函数.
的定义域是{x|x≠0},故两个函数不是同一个函数.同理D中的两个函数的定义域也不同.故不是同一个函数.
C.中的对应法则不同,故不是同一个函数.
B.∵g(x)=
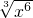 =x2,而f(x)=x2,∴函数f(x)与g(x)是同一个函数.
=x2,而f(x)=x2,∴函数f(x)与g(x)是同一个函数.故选B.
点评:本题考查两个函数是否是同一个函数,据确定一个函数的三要素(定义域、值域和对应法则)不难判断出.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
给出函数f(x)的一条性质:“存在常数M,使得|f(x)|≤M|x|对于定义域中的一切实数x均成立.”则下列函数中具有这条性质的函数是( )
A、y=
| ||
| B、y=x2 | ||
| C、y=x+1 | ||
| D、y=xsinx |