题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按
依次按![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项循环地分为
项循环地分为![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列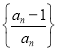 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() (2)3012 (3)
(2)3012 (3)![]()
【解析】
(1)求得![]() ,分别令
,分别令![]() ,2,3,进而归纳出数列
,2,3,进而归纳出数列![]() 的通项公式;
的通项公式;
(2)写出几个循环数,可得每一次循环记为一组,由每一个循环含有5个括号,故![]() 是第20组中第5个括号内的数之和,每一个循环中含有15个数,20个循环具有300个数,计算可得所求和;
是第20组中第5个括号内的数之和,每一个循环中含有15个数,20个循环具有300个数,计算可得所求和;
(3)由题意可得原不等式即为![]() 对一切
对一切![]() 都成立,
都成立,
设![]() ,则只需
,则只需![]() ,判断数列
,判断数列![]() 的单调性,可得最大值,解不等式即可得到所求
的单调性,可得最大值,解不等式即可得到所求![]() 的范围.
的范围.
![]() 因为点
因为点![]() 在函数
在函数![]() 的图象上,故
的图象上,故![]()
所以![]()
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
令![]() ,得
,得![]() ,所以
,所以![]() ;
;
由此猜想:![]() .
.
![]() 因为
因为![]() ,所以数列
,所以数列![]() 依次按
依次按![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项循环地分为
项循环地分为![]() ,
,![]() ,
,![]() ,
,
每一次循环记为一组.由于每一个循环含有![]() 个括号,故
个括号,故![]() 是第
是第![]() 组中第
组中第![]() 个括号内各数之和,每个循环中有
个括号内各数之和,每个循环中有![]() 个数,
个数,![]() 个循环共有
个循环共有![]() 个数.
个数.
![]()
![]()
又![]() ,所以
,所以![]() .
.
(3)因为![]() 故
故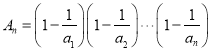 ,
,
所以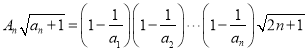
又![]()
故![]() 对一切
对一切![]() 都成立,
都成立,
就是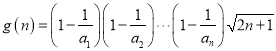 ,则只需
,则只需![]() 即可
即可
由于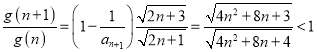 ,所以
,所以![]()
故![]() 是单调递减,
是单调递减,
于是![]() ,
,![]() 解得
解得![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了2018年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内,且月工资收入在
(百元)内,且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
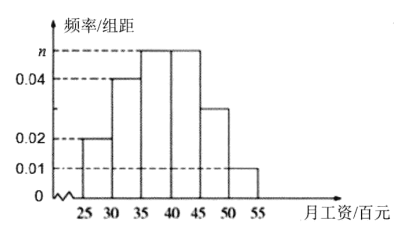
(1)求![]() 的值;
的值;
(2)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名.
名.
①完成如下所示![]() 列联表
列联表
技术工 | 非技术工 | 总计 | |
月工资不高于平均数 |
| ||
月工资高于平均数 |
| ||
总计 |
|
|
|
②则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: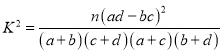 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校理科实验班的100名学生期中考试的语文、数学成绩都不低于100分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:[100,110),[110,120),[120,130),[130,140),[140,150].
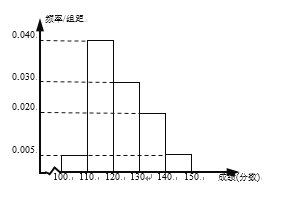
这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 | [100,110) | [110,120) | [120,130) | [130,140) |
| 1:2 | 2:1 | 3:4 | 1:1 |
(1)估计这100名学生语文成绩的平均数、方差(同一组数据用该区间的中点值作代表);
(2)从数学成绩在[130,150] 的学生中随机选取2人,该2人中数学成绩在[140,150]的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.