题目内容
(文)已知函数f(x)=x3+bx2+cx+d有两个极值点x1=1,x2=2,且直线y=6x+1与曲线y=f(x)相切于P点.
(1)求b和c
(2)求函数y=f(x)的解析式;
(3)在d为整数时,求过P点和y=f(x)相切于一异于P点的直线方程.
答案:
解析:
解析:
|
(文)解:(1)设直线y=6x+1,和y=x3+bx2+cx+d相切于点P(x0,y0) ∵f(x)=x3+bx2+cx+d有两个极值点x1=1,x2=2, 于是f'(x)=3x2+2bx+c=3(x-1)(x-2)=3x2-9x+6 从而b=- (2)又f(x)=x3- 由③求得x0=0或x0=3,由①②联立知d=1+ 时,d= (3)当d为整数时,d=1符合条件,此时P为(0,1) 设过P(0,1)的直线l:y=kx+1和y=x3- 再联立⑥可知k=x12-x1+6=3x12-9x1+6,又x1≠0, ∴x1= |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
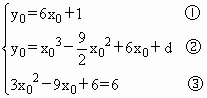
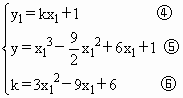 由④⑤及x1≠0,可知:kx1=x13-
由④⑤及x1≠0,可知:kx1=x13-