题目内容
如图,在?ABCD中,设E和F分别是边BC和AD的中点,BF和DE分别交AC于P、Q两点.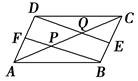
求证:AP=PQ=QC.
见解析
解析证明 ∵四边形ABCD是平行四边形,E、F分别是BC、AD边上的中点,
∴DF綉BE,∴四边形BEDF是平行四边形.
∵在△ADQ中,F是AD的中点,FP∥DQ.
∴P是AQ的中点,∴AP=PQ.
∵在△CPB中,E是BC的中点,EQ∥BP,
∴Q是CP的中点,∴CQ=PQ,∴AP=PQ=QC.

练习册系列答案
相关题目
题目内容
如图,在?ABCD中,设E和F分别是边BC和AD的中点,BF和DE分别交AC于P、Q两点.
求证:AP=PQ=QC.
见解析
解析证明 ∵四边形ABCD是平行四边形,E、F分别是BC、AD边上的中点,
∴DF綉BE,∴四边形BEDF是平行四边形.
∵在△ADQ中,F是AD的中点,FP∥DQ.
∴P是AQ的中点,∴AP=PQ.
∵在△CPB中,E是BC的中点,EQ∥BP,
∴Q是CP的中点,∴CQ=PQ,∴AP=PQ=QC.
