题目内容
设 、
、 ∈R且
∈R且 ,求
,求 的范围.
的范围.
 、
、 ∈R且
∈R且 ,求
,求 的范围.
的范围.0≤ ≤4.
≤4.
 ≤4.
≤4.解:方法一:等价转化法(转化为函数问题)
由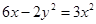 ≥0得0≤
≥0得0≤ ≤2.
≤2.
设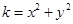 ,则
,则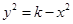 ,代入已知等式得:
,代入已知等式得: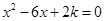 ,
,
即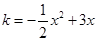 ,其对称轴为
,其对称轴为 =3.
=3.
由0≤ ≤2得
≤2得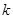 ∈[0,4].
∈[0,4].
所以 的范围是:0≤
的范围是:0≤ ≤4.
≤4.
方法二:数形结合法(转化为解几何问题):
由 得
得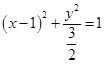 ,即表示如图所示椭圆,其一个顶点在坐标原点.
,即表示如图所示椭圆,其一个顶点在坐标原点. 的范围就是椭圆上的点到坐标原点的距离的平方.由图可知最小值是0,距离最大的点是以原点为圆心的圆与椭圆相切的切点.设圆方程为
的范围就是椭圆上的点到坐标原点的距离的平方.由图可知最小值是0,距离最大的点是以原点为圆心的圆与椭圆相切的切点.设圆方程为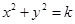 ,代入椭圆中消
,代入椭圆中消 得
得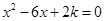 .由判别式
.由判别式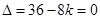 得
得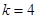 ,所以
,所以 的范围是:
的范围是: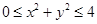 .
.
方法三: 三角换元法,对已知式和待求式都可以进行三角换元(转化为三角问题):
由 得
得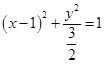 ,设
,设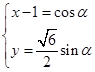 ,则
,则
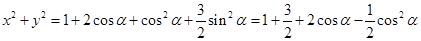
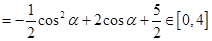
所以 的范围是:
的范围是: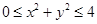 .
.
由
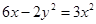 ≥0得0≤
≥0得0≤ ≤2.
≤2.设
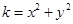 ,则
,则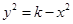 ,代入已知等式得:
,代入已知等式得: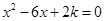 ,
,即
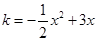 ,其对称轴为
,其对称轴为 =3.
=3.由0≤
 ≤2得
≤2得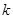 ∈[0,4].
∈[0,4].所以
 的范围是:0≤
的范围是:0≤ ≤4.
≤4.方法二:数形结合法(转化为解几何问题):
由
 得
得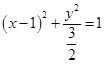 ,即表示如图所示椭圆,其一个顶点在坐标原点.
,即表示如图所示椭圆,其一个顶点在坐标原点. 的范围就是椭圆上的点到坐标原点的距离的平方.由图可知最小值是0,距离最大的点是以原点为圆心的圆与椭圆相切的切点.设圆方程为
的范围就是椭圆上的点到坐标原点的距离的平方.由图可知最小值是0,距离最大的点是以原点为圆心的圆与椭圆相切的切点.设圆方程为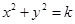 ,代入椭圆中消
,代入椭圆中消 得
得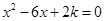 .由判别式
.由判别式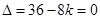 得
得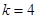 ,所以
,所以 的范围是:
的范围是: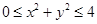 .
.方法三: 三角换元法,对已知式和待求式都可以进行三角换元(转化为三角问题):
由
 得
得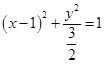 ,设
,设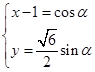 ,则
,则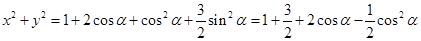
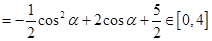
所以
 的范围是:
的范围是: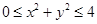 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则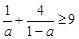
 ,则下列推证中正确的是( )
,则下列推证中正确的是( )

 ,
,

 ,且
,且 ,则 ( )
,则 ( )



 ,则( )
,则( ) ,则
,则
 ,则
,则
 ”是“
”是“ ”的( )
”的( )