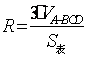题目内容
三棱锥
及其侧视图、俯视图如图所示.设
，
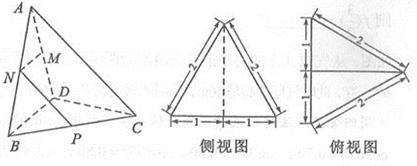
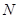分别为线段
，
的中点，
为线段
上的点，且
.
（1）证明：为线段的中点；
（2）求二面角
的余弦值.
（1）证明详见解析；（2）
.
解析试题分析：根据侧视图和俯视图可知，
为正三角形，顶点D在底面内的射影为BD的中点O，所以
两两互相垂直，故可以为坐标轴建立坐标系如图所示.（1）
，为了证明点P是BC的中点，只需利用向量证明
即可.（2）利用向量求出平面PMN和平面ABC的法向量，求出法向量的夹角即可得二面角的余弦值.
试题解答：取BD的中点O，建坐标系如图所示，则
，
，设（1）证明：设
，则
，
.因为
，所以点P是BC的中点.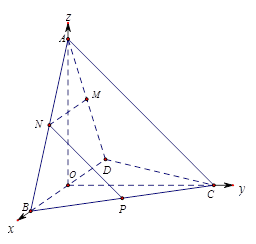
（2）易平面PMN的法向量为
.
，设平面ABC的法向量为
，则
，所以
.
【考点定位】1、空间直线与平面的位置关系；2、二面角.
练习册系列答案
相关题目
中，
⊥底面
，底面
，
，
分别是
，
的 中点．
平面
；
；
是线段
上一动点，试确定
平面
，并证明你的结论．
中,已知平面
平面
且
,
.
为棱
上的一点,且
平面
,求线段
的长度
-A BC中，AB 
AC，AB=AC=2，
=4，点D是BC的中点．
与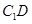
所成角的余弦值；
与
所成二面角的正弦值.
和
都为矩形。
，证明：直线
平面
，
分别是线段
，
的中点，在线段
上是否存在一点
，使直线
平面
？请证明你的结论。
，AA′＝1，点M，N分别为A′B和B′C′的中点．
Sh，其中S为底面面积，h为高)
