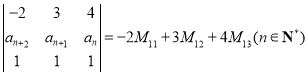题目内容
【题目】在
中，角
所对的边分别为
．向量
，
，且
（1）若
，求角
的值；
（2）求角
的最大值．
【答案】（1）
；（2）
.
【解析】
（1）利用向量平行得到
，再利用正弦定理化简，可求得
，从而求得
；（2）方法一：利用正弦定理将边都化成角的关系，化简求得
，再利用
，结合基本不等式求得
的最值，从而得到
的最大值；方法二：利用余弦定理将角化成边的关系，再利用
和基本不等式得到的最小值，从而得到的最大值.
（1）因为
，
，且
所以
，即
由正弦定理
，得
……①
所以
整理，得
……②
将
代入上式得
又
，所以
（2）方法一：由①式，因为
，
，所以
②式两边同时除以
，得
又
当且仅当
，即时取等号
又
，所以的最大值为
方法二：由（1）知，
由余弦定理
代入上式并化简得
所以
又
当且仅当
，即
时取等号
又，所以的最大值为
练习册系列答案
相关题目
