题目内容
已知函数f(x)=lnx-ax2+(2-a)x
(1)讨论f(x)的单调性;(2)设a>0,证明:当0<x< 时,f
时,f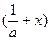 >f
>f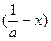 ;
;
(3)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明f′(x0)<0.
解:(1)f(x)的定义域为(0,+∞),f′(x)= -2ax+(2-a)= …1分
-2ax+(2-a)= …1分
①若a≤0,则f′(x)>0,所以f(x)在(0,+∞)单调递增.…………2分
②若a>0,则由f′(x)=0得x= ,且当x∈(0,
,且当x∈(0,  )时,f′(x)>0,当x>
)时,f′(x)>0,当x> 时,
时,
f′(x)<0.所以f(x)在(0,  )单调递增
)单调递增 ,在(
,在( ,
, )单调递减.…………4分
)单调递减.…………4分
(2)设函数g(x)=f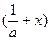 -f
-f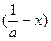 ,则g(x)=ln(1+ax)-ln(1-ax)-2ax,
,则g(x)=ln(1+ax)-ln(1-ax)-2ax,
g′(x)=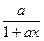 +
+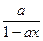 -2a …………………………6分
-2a …………………………6分
当0<x< 时,g′(x)>0,…………7分 而g(0)=0,所以g(x)>0.
时,g′(x)>0,…………7分 而g(0)=0,所以g(x)>0.
故当0<x< 时,f
时,f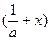 >f
>f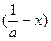 . …………………………9分
. …………………………9分
(3)当a≤0时,函数y=f(x)的图象与x轴至多有一 个交点,故a>0,…………10分
个交点,故a>0,…………10分
从而f(x)的最大值为 ,且
,且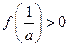 .…………………………11分
.…………………………11分
不妨设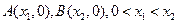 ,则
,则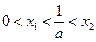 .
. 由(2)得
由(2)得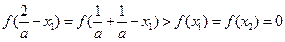 ,而f(x)在(
,而f(x)在( ,
, )单调递减.
)单调递减.
∴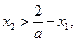 ……14分于是
……14分于是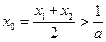 .由(1)知,
.由(1)知,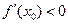 .…………15分
.…………15分
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 定义域为
定义域为 (
( ),设
),设 .
. 的取值范围,使得函数
的取值范围,使得函数 在
在 ;
; ,总存在
,总存在 ,满足
,满足 ,并确定这样的
,并确定这样的 的个数.
的个数.
 ,其中a为常数.
,其中a为常数. 的一个极值点,求a的值;
的一个极值点,求a的值; ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围. 设g(x)=f(x)-2x2,求证函数g(x)只有一个零点.
设g(x)=f(x)-2x2,求证函数g(x)只有一个零点. (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方 -bx+4,当x=2时,函数f(x)有极值-.
-bx+4,当x=2时,函数f(x)有极值-. 在
在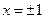 处取得极值。
处取得极值。 的解析式;
的解析式; Ⅱ)求证:对于区间
Ⅱ)求证:对于区间 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。 元)与隔热层厚度x(单位:cm)
元)与隔热层厚度x(单位:cm) ②若不建隔热层,每年能源消耗费用为8万
②若不建隔热层,每年能源消耗费用为8万