题目内容
已知函数![]() ,在点(1,f(1))处的切线方程为y+2=0.
,在点(1,f(1))处的切线方程为y+2=0.
(1) 求函数f(x)的解析式;
(2) 若对于区间[一2,2]上任意两个自变量的值x1,x2,都有![]() ,求实
,求实
数c的最小值;
(3) 若过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线,求实数m的取值范围。
解:(1)![]() …………1分
…………1分
根据题意,得![]() 即
即![]() 解得
解得![]() ………3分
………3分
∴f(x)=x3-3x. . ………………4分
(2)令f'(x)= 3x2-3=O,即3x2-3=O,解得x=±1.

∵f(-1)=2,f(1)=-2,∴当x∈[-2,2]时,f(x)max=2,f(x)min=-2.
则对于区间[-2,2]上任意两个自变量的值x1,x2,都有
![]() ,所以c≥4.
,所以c≥4.
所以c的最小值为4. …………………8分
(3)∵点M(2,m)(m≠2)不在曲线y=f(x)上,∴设切点为(x0,y0).则![]()
![]() ,∴切线的斜率为
,∴切线的斜率为![]()
则![]() ,即
,即![]()
因为过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线,
所以方程![]() 有三个不同的实数解.
有三个不同的实数解.
即函数g(x)= 2x3-6x2+6+m有三个不同的零点.
则g'(x)=6x2-12x.令g'(x)=0,解得x=O或x=2.

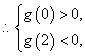 即
即![]() 解得-6<m<2. ……………………l4分[来源:Z,xx,k.Com]
解得-6<m<2. ……………………l4分[来源:Z,xx,k.Com]

练习册系列答案
相关题目
 , 已知函数
, 已知函数
 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;  在点
在点 处的切线相互平行, 且
处的切线相互平行, 且 证明
证明 .
. ,在点
,在点 处的切线方程是
处的切线方程是 (e为自然对数的底)。
(e为自然对数的底)。 的值及
的值及 的解析式;
的解析式; 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值; 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 ,在点(1,f(1))处的切线方程为y+2=0.
,在点(1,f(1))处的切线方程为y+2=0.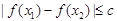 ,求实
,求实