题目内容
设 , 已知函数
, 已知函数
(Ⅰ) 证明 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
(Ⅱ) 设曲线 在点
在点 处的切线相互平行, 且
处的切线相互平行, 且 证明
证明 .
.
【答案】
见解析
【解析】(Ⅰ)证明:设函数 ,
, ,
,
① ,因为
,因为 ,所以当
,所以当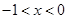 时,
时,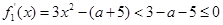 ,
,
所以函数 在区间(-1,0)内单调递减;
在区间(-1,0)内单调递减;
② ,因为
,因为 ,所以当
,所以当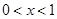 时,
时,
 ;当
;当 时,
时, ,即函数
,即函数 在区间(0,1)内单调递减,在区间
在区间(0,1)内单调递减,在区间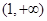 内单调递增.
内单调递增.
综合①②及 ,可知函数
,可知函数 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增.
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增.
(Ⅱ)证明:由(Ⅰ)知,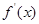 在区间
在区间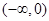 内单调递减,在区间
内单调递减,在区间 内单调递减,在区间
内单调递减,在区间
 内单调递增.因为曲线
内单调递增.因为曲线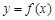 在点
在点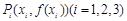 处的切线相互平行,从而
处的切线相互平行,从而 互不相等,且
互不相等,且 .不妨设
.不妨设 ,
,
由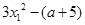 =
= =
=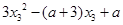 ,可得
,可得
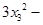
 ,
,
解得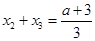 ,从而
,从而 ,
,
设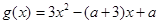 ,则
,则 ,
,
由 =
=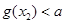 ,解得
,解得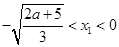 ,所以
,所以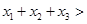
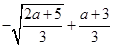 ,
,
设 ,则
,则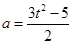 ,因为
,因为 ,所以
,所以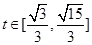 ,
,
故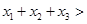
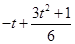 =
=
 ,即
,即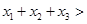
 .
.
本题第(Ⅰ)问,可以分两段来证明,都是通过导数的正负来判断单调性;第(Ⅱ)问,由切线平行知,切线的斜率相等,然后构造函数解决.判断分段函数的单调性时,要分段判断;证明不等式时,一般构造函数解决.
【考点定位】本小题主要考查导数的运算及其几何意义,利用导数研究函数的单调性,考查分类讨论思想、化归思想、函数思想,考查综合分析问题和解决问题的能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
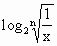 (n∈N).
(n∈N).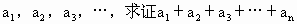 <1;
<1; 为已知函数的图像上与x轴距离为1的两点,求证:n取任意一个正整数时,以
为已知函数的图像上与x轴距离为1的两点,求证:n取任意一个正整数时,以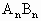 为直径的圆都与一条定直线相切,并求出这条定直线的方程和切点的坐标.
为直径的圆都与一条定直线相切,并求出这条定直线的方程和切点的坐标. ,已知函数
,已知函数 的定义域是
的定义域是 ,值域是
,值域是 ,若函数
,若函数 ( )
( ) C.1
D.0
C.1
D.0