题目内容
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是正方形,且四个侧面均为等边三角形.延长
是正方形,且四个侧面均为等边三角形.延长![]() 至点
至点![]() 使
使![]() ,连接
,连接![]() ,
,![]() .
.

(1)证明:![]() ;
;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,推导出
,推导出![]() 平面
平面![]() ,从而
,从而![]() ,由此能证明
,由此能证明![]() .
.
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(1)连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,如图
,如图
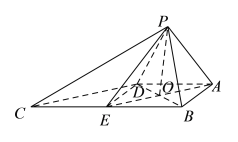
∵底面![]() 是正方形
是正方形
∴![]()
∵四棱锥![]() 中四个侧面均为等边三角形
中四个侧面均为等边三角形
∴![]()
又![]() ,故
,故![]() 为
为![]() 、
、![]() 的中点
的中点
∴![]()
∵![]()
∴![]() 平面
平面![]()
∵![]() ,
,![]() 为
为![]() 的中点
的中点
∴![]()
∴![]() 平面
平面![]()
∴![]()
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
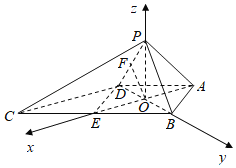
设![]() ,则
,则![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,
,
![]() ,0,
,0,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则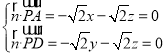 ,取
,取![]() ,得
,得![]() ,1,
,1,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则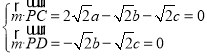 ,取
,取![]() ,得
,得![]() ,1,
,1,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() .
.
观察图形知二面角![]() 的平面角为钝角
的平面角为钝角
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知某公司成本为![]() 元,所得的利润
元,所得的利润![]() 元的几组数据入下.
元的几组数据入下.
第一组 | 第二组 | 第三组 | 第四组 | 第五组 | |
| 1 | 4 | 5 | 2 | 3 |
| 2 | 1 | 3 | 4 | 0 |
根据上表数据求得回归直线方程为:![]()
(1)若这个公司所规划的利润为200万元,估算一下它的成本可能是多少?(保留1位小数)
(2)在每一组数据中,![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() ;
;![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() ;
;![]() ,
,![]() 相差
相差![]() ,记为事件
,记为事件![]() .随机抽两组进行分析,则抽到有事件
.随机抽两组进行分析,则抽到有事件![]() 发生的概率.
发生的概率.

